Optimaal voorraadbeheer in een fluctuerende markt€¦ · 1.4 Evolutie van de voorraad in de tijd...
Transcript of Optimaal voorraadbeheer in een fluctuerende markt€¦ · 1.4 Evolutie van de voorraad in de tijd...

UNIVERSITEIT GENT
FACULTEIT ECONOMIE EN BEDRIJFSKUNDE
ACADEMIEJAAR 2011 – 2012
Optimaal voorraadbeheer in een fluctuerende markt
Masterproef voorgedragen tot het bekomen van de graad van
Master of Science in de
Toegepaste Economische Wetenschappen: Handelsingenieur
Willem Hendrickx
onder leiding van
Prof. dr. ir. H. Bruneel
Prof. dr. ing. D. Fiems
Thesisbegeleiders:
Ir. Eline De Cuypere
Dr. ir. Wouter Rogiest


UNIVERSITEIT GENT
FACULTEIT ECONOMIE EN BEDRIJFSKUNDE
ACADEMIEJAAR 2011 – 2012
Optimaal voorraadbeheer in een fluctuerende markt
Masterproef voorgedragen tot het bekomen van de graad van
Master of Science in de
Toegepaste Economische Wetenschappen: Handelsingenieur
Willem Hendrickx
onder leiding van
Prof. dr. ir. H. Bruneel
Prof. dr. ing. D. Fiems
Thesisbegeleiders:
Ir. Eline De Cuypere
Dr. ir. Wouter Rogiest

PERMISSION
Ondergetekende verklaart dat de inhoud van deze masterproef mag geraadpleegd en/of gereprodu-ceerd worden, mits bronvermelding.
Willem Hendrickx

Woord vooraf
Deze masterproef is het sluitstuk van de vijfjarige opleiding Toegepaste Economische Weten-schappen: Handelsingenieur aan de Universiteit Gent. Graag zou ik iedereen willen bedanken dieheeft bijgedragen tot de verwezenlijking van dit eindwerk. Vooreerst mijn oprechte dank aan prof.dr. ing. Dieter Fiems, ir. Eline De Cuypere en dr. ir. Wouter Rogiest. Zij hebben mij gedurende delaatste twee jaar met raad en daad bijgestaan en hun raadgevingen en kennis zijn van goudwaardegeweest. Eveneens wil ik mijn dank betuigen aan prof. dr. ir. Herwig Bruneel voor het beschik-baar stellen van dit onderwerp en voor het op zich nemen van de taak van promotor. Ten slotte nogeen speciaal woord van dank aan mijn ouders voor de morele steun en aan mijn zus Mieke voorhet nalezen van mijn eindwerk.
Dank u wel,
Willem Hendrickx
Gent, 8 augustus 2012
I

Inhoudsopgave
Woord vooraf I
Lijst van figuren IV
Lijst van tabellen VI
Inleiding 1
1 Probleemstelling 41.1 Voorraadbeheer . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.1.1 Kosten verbonden aan het houden van voorraad . . . . . . . . . . . . . . 81.1.2 Modellen voor voorraadbeheer . . . . . . . . . . . . . . . . . . . . . . . 9
1.2 Specifieke uitdagingen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
2 Onderzoeksaanpak 172.1 Methodologie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
2.1.1 Markov-ketens . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 172.1.2 Lange-termijn eigenschappen van een Markov-keten . . . . . . . . . . . 192.1.3 Markoviaanse beslissingsprocessen . . . . . . . . . . . . . . . . . . . . 20
2.2 Oplossingsmethodes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 232.2.1 Lineair programmeren . . . . . . . . . . . . . . . . . . . . . . . . . . . 252.2.2 Policy iteration . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 262.2.3 Modified policy iteration . . . . . . . . . . . . . . . . . . . . . . . . . . 272.2.4 Value iteration . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 272.2.5 Gauss-Seidel value iteration . . . . . . . . . . . . . . . . . . . . . . . . 28
2.3 Het toepassen van deze theorie doorheen de masterproef . . . . . . . . . . . . . 29
3 Inleidend model met een beperkte toestandsruimte 323.1 Inleiding . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 323.2 Model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
3.2.1 Markov-ketens . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 333.2.2 Eigenschappen van beide Markov-ketens . . . . . . . . . . . . . . . . . 363.2.3 Markoviaans beslissingsproces . . . . . . . . . . . . . . . . . . . . . . . 383.2.4 Transitiematrices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
II

3.2.5 Kostmatrices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 443.3 Resultaten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
3.3.1 Invloed van de prijs op het bestelbeleid . . . . . . . . . . . . . . . . . . 463.3.2 Invloed van de voorraadkost op het bestelbeleid . . . . . . . . . . . . . . 473.3.3 Invloed van de bestelkost op het bestelbeleid . . . . . . . . . . . . . . . 473.3.4 Invloed van de prijsevolutie op het bestelbeleid . . . . . . . . . . . . . . 483.3.5 Vergelijking van de verschillende oplossingsmethodes . . . . . . . . . . 49
4 Model met een uitgebreide toestandsruimte 504.1 Inleiding . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 504.2 Model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
4.2.1 Markov-keten voorraadniveau . . . . . . . . . . . . . . . . . . . . . . . 524.2.2 Markov-keten prijsniveau . . . . . . . . . . . . . . . . . . . . . . . . . 524.2.3 Volledige Markov-keten . . . . . . . . . . . . . . . . . . . . . . . . . . 574.2.4 Markoviaans beslissingsproces . . . . . . . . . . . . . . . . . . . . . . . 57
4.3 Resultaten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 584.3.1 Invloed van de prijs op het bestelbeleid . . . . . . . . . . . . . . . . . . 584.3.2 Vergelijking van de verschillende oplossingsmethodes . . . . . . . . . . 614.3.3 Invloed van de bestelkost op het bestelbeleid . . . . . . . . . . . . . . . 634.3.4 Invloed van de disconteringsfactor op het bestelbeleid . . . . . . . . . . 634.3.5 Invloed van de vraag op het bestelbeleid . . . . . . . . . . . . . . . . . . 644.3.6 Invloed van de prijsfluctuaties op het bestelbeleid . . . . . . . . . . . . . 65
5 Model met een onzekere levertermijn 685.1 Inleiding . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 685.2 Model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
5.2.1 Levertermijn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 705.2.2 De kost van verloren vraag . . . . . . . . . . . . . . . . . . . . . . . . . 73
5.3 Resultaten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 745.3.1 Gevolgen van het invoeren van een onzekere levertermijn . . . . . . . . . 745.3.2 Invloed van de kost van verloren vraag op het bestelbeleid . . . . . . . . 765.3.3 Vergelijking van de verschillende oplossingsmethodes . . . . . . . . . . 78
Conclusies en verder onderzoek 80
Bibliografie i
Appendix A Lijst van de gebruikte symbolen iii
III

Lijst van figuren
1.1 Relevante voorraad-gerelateerde kosten en de economische bestelhoeveelheid . . 121.2 Evolutie in de tijd van het voorraadniveau met de formule van Camp . . . . . . . 131.3 Evolutie van de voorraad in de tijd met constante levertermijn en deterministische
vraag . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 131.4 Evolutie van de voorraad in de tijd met stochastische vraag en lead time . . . . . 14
2.1 In het policy iteration algoritme voor het oplossen van Markoviaanse beslissings-processen is er een continue interactie tussen beleids- en waardefuncties die stoptwanneer hun optimale waardes bereikt worden [20] . . . . . . . . . . . . . . . . 27
3.1 Geometrische verdeelde vraag . . . . . . . . . . . . . . . . . . . . . . . . . . . 353.2 Grafische voorstelling van de vraagfluctuaties door middel van een Markov-keten 353.3 Grafische voorstelling van de prijsfluctuaties door middel van een Markov-keten . 363.4 Grafische voorstelling van de marktfluctuaties door middel van een Markov-keten 373.5 Mogelijke acties en overgangen in het Markoviaans beslissingsproces . . . . . . 403.6 Mogelijke transities na het kiezen van actie d2 . . . . . . . . . . . . . . . . . . . 403.7 Invloed van de prijs op het bestelbeleid . . . . . . . . . . . . . . . . . . . . . . . 473.8 Invloed van de voorraadkost op het bestelbeleid . . . . . . . . . . . . . . . . . . 483.9 Invloed van de bestelkost op het bestelbeleid . . . . . . . . . . . . . . . . . . . . 48
4.1 Voorbeeld van een mogelijk voorraadverloop in het uitgebreide model . . . . . . 514.2 Grafische voorstelling van de vraagfluctuaties door middel van een Markov-keten 524.3 Grafische voorstelling van de prijsfluctuaties door middel van een Markov-keten . 534.4 Mogelijke kansverdelingen voor het prijsniveau in functie van α en β . . . . . . 544.5 Mogelijke kansverdelingen voor het prijsniveau in functie van v . . . . . . . . . 554.6 Simulatie van de evolutie van het prijsniveau in de tijd voor verschillende waarden
van v . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 564.7 Mogelijke acties en de gevolgen . . . . . . . . . . . . . . . . . . . . . . . . . . 584.8 Invloed van de het prijs- en voorraadniveau op het bestelbeleid . . . . . . . . . . 594.9 Invloed van de prijs op het bestelbeleid in het laagste voorraadniveau . . . . . . . 604.10 Overzicht van de oplossingstijden van de verschillende oplossingsmethodes in
functie van het aantal toestanden . . . . . . . . . . . . . . . . . . . . . . . . . . 624.11 Invloed van de bestelkost C0 op het bestelbeleid . . . . . . . . . . . . . . . . . . 634.12 Invloed van de disconteringsfactor d op het bestelbeleid . . . . . . . . . . . . . . 64
IV

4.13 Invloed van de kans op vraag op het bestelbeleid . . . . . . . . . . . . . . . . . . 654.14 Invloed van de frequentie van de prijsfluctuaties op het bestelbeleid . . . . . . . . 654.15 Invloed van de factor v op het bestelbeleid . . . . . . . . . . . . . . . . . . . . . 67
5.1 Kansverdeling van de levertermijn en de gemiddelde levertermijn bij verschillendewaarden voor κ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
5.2 Het introduceren van een extra dimensie in voorraadniveau N met als doel hetmodelleren van een variabele levertermijn . . . . . . . . . . . . . . . . . . . . . 71
5.3 Illustratie van het model met levertermijn aan de hand van een voorbeeld . . . . . 725.4 Het introduceren van een fictief voorraadniveau −1 in de Markov-keten . . . . . 735.5 Effect van het invoeren van een onzekere levertermijn op het bestelbeleid . . . . 755.6 De invloed van de kans op levering κ op de ’besteldrempel’ . . . . . . . . . . . . 765.7 Invloed van de kost van verloren vraag Cv op het bestelbeleid . . . . . . . . . . . 775.8 Gevolgen op het bestelbeleid van de combinatie van een hoge kost van verloren
vraag en een lage kans op levering . . . . . . . . . . . . . . . . . . . . . . . . . 775.9 Overzicht van de oplossingstijden van de verschillende oplossingsmethodes in
functie van het aantal toestanden . . . . . . . . . . . . . . . . . . . . . . . . . . 78
V

Lijst van tabellen
1.1 Bijdrage van diverse kostencategorieen tot de totale voorraadkost volgens Richard-son (1995) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
1.2 Gebruikte parameters en variabelen in de formule van Camp . . . . . . . . . . . 11
3.1 Gebruikte parameters in het vereenvoudigde model . . . . . . . . . . . . . . . . 343.2 Overzicht van de mogelijke toestanden Si waarin het systeem zich kan bevinden . 363.3 Gebruikte parameters in het vereenvoudigde model . . . . . . . . . . . . . . . . 393.4 Invloed van de prijs op het bestelbeleid . . . . . . . . . . . . . . . . . . . . . . . 463.5 Vergelijking van de verschillende oplossingsmethodes . . . . . . . . . . . . . . . 49
4.1 Overzicht en definitie van de nieuwe parameters en variabelen in hoofdstuk 4 . . 524.2 Volledige toestandsruimte van het uitgebreide model . . . . . . . . . . . . . . . 574.3 Arbitrair gekozen parameters voor het oplossen van het uitgebreide model . . . . 594.4 Vergelijking van de verschillende oplossingsmethodes in een 4×2, respectievelijk
20× 20 toestandsruimte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
5.1 Overzicht van de gebruikte variabelen en parameters . . . . . . . . . . . . . . . 70
VI

Inleiding
De probleemstelling van deze masterproef situeert zich in het domein van het voorraadbeheer. Het
doel omvat het uitwerken van een wiskundig model dat de uitgesproken dynamiek van een voor-
raadbeheersysteem kan vatten. Bij klassiek voorraadbeheer zal men de voorraad van een bepaald
product aanvullen op vaste tijdstippen of van zodra het voorraadniveau onder een bepaalde drem-
pelwaarde zakt, zoals bij het bekende ’Economic Order Quantity’-model het geval is. Aan de hand
van het EOQ-model kan men deze drempelwaarde en de bestelhoeveelheid bepalen die de totale
kost verbonden aan het houden van voorraad minimaliseren. Deze klassieke modellen zijn echter
niet altijd optimaal. Er worden namelijk een aantal veronderstellingen gemaakt die niet altijd even
realistisch zijn, zoals een deterministische omgeving. Het gebruik van dit klassieke EOQ-model in
een stochastische en dynamische omgeving levert, ondanks de robuustheid van het model, dan ook
weinig accurate resultaten op. Er zijn bijgevolg tal van uitbreidingen terug te vinden in de litera-
tuur, die in min of meerdere mate de dynamiek van een werkelijk voorraadbeheersysteem kunnen
vatten. Elk model bevat echter enkele vereenvoudigende veronderstellingen van de werkelijkheid
waardoor de praktische toepasbaarheid beperkt wordt tot zeer specifieke situaties.
Ook deze masterproef richt zich op een zeer specifieke bedrijfssituatie en bevat belangrijke ver-
onderstellingen die de complexiteit van het model enigszins beperken. De concrete uitdaging
die in deze masterproef wordt aangegaan is het integreren van marktfluctuaties in een wiskundig
model, en dit in een stochastische omgeving. In het bijzonder wordt een voorraadbeheer-model
bestudeerd waarbij het aankoopgedrag niet enkel afhankelijk is van een fluctuerend voorraadni-
veau, maar ook van een fluctuerende marktprijs. De mogelijkheid om aan een relatief goedkope
prijs aan te kopen weegt mogelijk op tegen een hogere voorraadkost. Dit impliceert dat bij iedere
mogelijke combinatie van prijs- en voorraadniveau een beslissing moet worden genomen omtrent
enerzijds het al dan niet bestellen en anderzijds de bestelhoeveelheid.
De invloed van vraagfluctuaties is reeds uitgebreid onderzocht als een uitbreiding van het klassieke
EOQ-model. De invloed van prijsfluctuaties daarentegen is nog een wetenschappelijk weinig ont-
gonnen terrein. Ter verduidelijking, onder de term fluctuaties bedoelen we in deze masterproef
korte- of middellange-termijn fluctuaties rond een lange-termijn gemiddelde. Het model is bij-
1

gevolg niet van toepassing op continu in prijs dalende of stijgende goederen, zoals bijvoorbeeld
hightech producten in de IT sector. Lange-termijn-fluctuaties (conjunctuur) vallen eveneens buiten
het bereik van het model. Wat betreft de vraagfluctuaties is dit model hoofdzakelijk toepasbaar op
producten in de maturiteitsfase, waar de gemiddelde vraag als constant kan worden verondersteld.
In deze masterproef zal een wiskundig voorraadbeheer-model ontwikkeld en besproken worden
waarbij een optimaal bestelbeleid wordt uitgewerkt voor de hierboven besproken situatie. Zowel
de fluctuerende aankoopprijs als de fluctuerende vraag zullen gemodelleerd worden in een sto-
chastische omgeving, door middel van een discrete, stationaire Markov-keten. Met behulp van de
theorie van de Markoviaanse beslissingsprocessen kan vervolgens een optimaal prijs afhankelijk
bestelbeleid bepaald worden, waarbij de lange-termijn verdisconteerde kost wordt geminimali-
seerd. De belangrijkste kosten waarmee moet rekening gehouden worden, zijn de aankoopkosten,
de vaste bestelkosten, de kosten ten gevolge van verloren vraag en de kosten voor het houden van
voorraad (opportuniteits- en opslagkosten). Bij het nemen van een beslissing omtrent de bestel-
hoeveelheid moet steeds een afweging gemaakt worden tussen deze verschillende categorieen van
kosten. De theorie der Markoviaanse beslissingsprocessen is een krachtig hulpmiddel voor het
optimaliseren van de prestaties van stochastische processen, die kunnen gemodelleerd worden als
een discrete tijd Markov-keten.
Op basis van de resultaten van dit onderzoek zal getracht worden algemeen geldende kwalitatieve
conclusies te formuleren. Zo zullen er bijvoorbeeld verscheidene scenario’s bekeken worden wat
betreft de prijsfluctuaties. Aangezien de wetten van het voorraadbeheer vrij logisch in elkaar zitten,
worden er in deze masterproef evenwel geen baanbrekende resultaten verwacht. Het doel van deze
masterproef is echter niet het ontdekken van nieuwe wetmatigheden, maar eerder het ontwikkelen
van een model dat toepasbaar is op een specifieke bedrijfssituatie die nog niet besproken werd in
de bestaande literatuur.
De structuur van deze masterproef ziet er als volgt uit: in hoofdstukken 1 en 2 wordt de theorie
aangehaald en uitgelegd die noodzakelijk is om de wiskundige modellen die in het licht van deze
masterproef zijn ontwikkeld te kunnen begrijpen. Tevens wordt toegelicht hoe deze theorie zal
toegepast worden en welke specifieke situaties zullen besproken worden. In hoofdstuk 1 worden
enkele relevante aspecten van het voorraadbeheer besproken. In hoofdstuk 2 worden de methodes
uiteengezet die toegepast zullen worden voor het modelleren, oplossen en analyseren van deze
probleemstelling. Dit hoofdstuk omvat de theorie omtrent Markov-ketens en Markoviaanse be-
slissingsprocessen. In hoofdstuk 3 wordt vervolgens op basis van deze theorie en de gemaakte
veronderstellingen een eerste eenvoudig model opgesteld waarbij slechts met een beperkte toe-
standsruimte zal gewerkt worden. In hoofdstuk 4 wordt de toepasbaarheid van het model vergroot
2

door deze toestandsruimte sterk uit te breiden. In hoofdstuk 5 wordt de praktische toepasbaarheid
nog verder vergroot door het introduceren van een onzekere levertermijn in het model.
Er werd gekozen voor deze stapsgewijze opbouw van het model omdat dit de overzichtelijkheid
sterk vergroot bij het uiteenzetten van de verscheidene aspecten van het model en omdat op deze
manier de negatieve invloed van een onzekere levertermijn op de prestaties van een voorraadbe-
heersysteem expliciet wordt weergegeven.
3

Hoofdstuk 1
Probleemstelling
De probleemstelling van deze masterproef situeert zich in het domein van het voorraadbeheer.
Bijgevolg wordt in dit eerste hoofdstuk een beknopte uiteenzetting gegeven van de verschillende
aspecten van het voorraadbeheer, de kosten die onlosmakelijk verbonden zijn met het houden van
voorraad en de bekendste modellen die reeds ontwikkeld zijn in dit domein. Elk model wordt ech-
ter gekenmerkt door een aantal beperkende veronderstellingen die ervoor zorgen dat de praktische
toepasbaarheid gelimiteerd is tot een aantal specifieke situaties. Het is dan ook van vitaal belang
steeds te onderzoeken welke veronderstellingen gelden voor een bepaald bedrijf. Ook in deze
masterproef wordt een wiskundig model ontwikkeld dat slechts toepasbaar is in zeer specifieke
situaties, maar deze specificiteit brengt ook een grotere nauwkeurigheid met zich mee indien de
desbetreffende veronderstellingen een goede representatie zijn van de werkelijkheid.
Het vervolg van dit inleidende hoofdstuk heeft de volgende structuur. In sectie 1.1 wordt een
korte inleiding gegeven tot het voorraadbeheer alsook enkele belangrijke modellen die als doel
hebben dit voorraadbeheer zo efficient mogelijk te laten verlopen of met andere woorden om zo
laag mogelijke voorraadkosten te bewerkstelligen. In sectie 1.2 wordt vervolgens de specifieke
omgeving toegelicht waarin het voorraadbeheermodel in deze masterproef van toepassing is. Hier
worden bijgevolg de contextuele veronderstellingen gemaakt die verder zullen worden uitgewerkt
in de volgende hoofdstukken.
1.1 Voorraadbeheer
In de uiterst competitieve omgeving waarin bedrijven zich vandaag bevinden, is het meer dan ooit
van belang dat de ondersteunende processen zoals voorraadbeheer zo efficient mogelijk verlopen.
Afhankelijk van het type onderneming kan de kost voor het houden van voorraad immers grote pro-
porties aannemen, terwijl deze processen in de meeste gevallen geen toegevoegde waarde brengen.
4

Elk bedrijf heeft er dan ook belang bij deze processen zo kostenefficient mogelijk te organiseren.
Hierbij moet rekening gehouden worden met enkele fundamentele trade-offs, zoals de afweging
tussen een lagere voorraadkost en een hogere ’service level’ of ’servicegraad’. Een tekort aan
voorraad kan immers ook hoge kosten met zich meebrengen, zowel kwalitatief als kwantitatief.
Voorraad is prominent aanwezig doorheen de volledige ’supply chain’ of ’toeleveringsketen’ en
ontstaat over het algemeen ten gevolge van een onevenwicht tussen vraag en aanbod, of met andere
woorden ten gevolge van een verschil in timing van beide. Niet enkel de onzekere vraag is hier van
groot belang, maar vaak is dit onevenwicht ook bewust gecreeerd. Omwille van de bestelkosten is
het immers voordeliger om in hoeveelheden groter dan een aan te kopen. Hierbij wordt immers de
kost per eenheid gedrukt door gebruik te maken van eventuele schaalvoordelen in de productie of
distributie van de goederen. Bovendien vergroot het houden van voldoende voorraad het service
level dat kan aangeboden worden aan de klant en ten gevolgde daarvan ook de klanttevredenheid.
Het behaalde service level wordt gegeven door de product-beschikbaarheid en wordt vaak gemeten
met behulp van de ’cycle service level’ 1, de ’product fill rate’ 2 of de ’order fill rate’ 3 [2, Hoofd-
stuk 11]. In de beginnende literatuur werd hoofdzakelijk de cycle service level gebruikt, maar in
de meer recente literatuur wordt hoofdzakelijk de product fill rate toegepast omdat deze maatstaf
een meer realistisch beeld geeft van het service level. Deze maatstaf houdt namelijk ook rekening
met de bestelgrootte. In deze masterproef zijn beide maatstaven aan elkaar gelijk aangezien een
bestelling steeds bestaat uit een eenheid.
Wat betreft schaalvoordelen vermelden Chopra en Meindl [2, Hoofdstuk 10] drie verschillende
situaties:
1. De vaste bestelkost, onafhankelijk van de bestelde hoeveelheid
2. Hoeveelheidskortingen als grote hoeveelheden worden aangekocht
3. Korte-termijn prijskortingen
In deze masterproef zal enkel rekening gehouden worden met de schaalvoordelen bij het bestellen
als gevolg van een vaste bestelkost. Indien ook hoeveelheidskortingen in het model zouden worden
opgenomen, zou de bestelhoeveelheid steeds groter zijn dan in het geval deze niet worden opgeno-
men. Kopers gaan immers gebruik maken van de vermindering in prijs, althans zolang dit voordeel
groter is dan het verschil in voorraadkost. Hoeveelheidskortingen kunnen bovendien ook zorgen
voor een betere coordinatie tussen de verschillende fases in een supply chain. Vaak is het immers
zo dat de optimale bestelhoeveelheid voor de koper verschilt van de optimale bestelhoeveelheid1Gedeelte van de voorraadaanvulling-cycli zonder ’stockout’ (voorraadtekort)2Gedeelte van de vraag waaraan voldaan wordt met de in voorraad aanwezige goederen3Gedeelte van de bestellingen waaraan voldaan wordt met de in voorraad aanwezige goederen
5

voor de verkoper. Hoeveelheidskortingen of ’two-part tariffs’ 4 kunnen er in dit geval voor zorgen
dat er besteld wordt in hoeveelheden die de winst in de totale supply chain maximaliseren, dit in
tegenstelling tot ’locale optimalisatie’ 5.
De fundamentele trade-off in voorraadbeheer is deze tussen kostenefficientie en flexibiliteit of re-
actiesnelheid [2, Hoofdstuk 3]. Door het aanhouden van een grote voorraad dicht bij de consument
zal het bedrijf sneller kunnen inspelen op de noden van de klanten. Bovendien kan in deze situ-
atie geprofiteerd worden van eventuele schaalvoordelen. Het aanhouden van een kleine voorraad
daarentegen brengt minder voorraadkosten met zich mee, maar kan als gevolg hebben dat klanten
(intern of extern) gedurende een lange tijd moeten wachten vooraleer aan hun verzoek kan voldaan
worden. Afhankelijk van de exclusiviteit van een product bestaat dan ook het risico dat deze klan-
ten elders hetzelfde product gaan inkopen waardoor er vraag verloren gaat. De grote uitdaging in
het efficient beheren van voorraad is bijgevolg het verminderen van de hoeveelheid goederen in
voorraad zonder dat de kosten stijgen of de reactiesnelheid daalt.
De flexibiliteit of reactiesnelheid wordt voor een groot deel bepaald door de doorstroomtijd van
materialen, een grootheid die weergeeft hoe lang materialen zich in de supply chain bevinden.
Volgens de wet van Little (zie formule (1.1)) is deze doorlooptijd bovendien recht evenredig met
de hoeveelheid voorraad die aangehouden wordt [2, Hoofdstuk 3]. Een groter aantal eenheden in
voorraad zorgt bijgevolg voor een langere doorlooptijd hetgeen de flexibiliteit van een supply chain
schaadt. In de wet van Little stelt de ’throughput’ het aantal verkochte eenheden per tijdseenheid
voor.
V oorraad = Throughput×Doorlooptijd (1.1)
Ook de product-beschikbaarheid, bijvoorbeeld gemeten door de cycle service level of order fill
rate, heeft vanzelfsprekend een belangrijke invloed op zowel de kostenefficientie als de flexibiliteit.
Een hoge product-beschikbaarheid, als gevolg van het aanhouden van een grote voorraad, heeft een
hoge flexibiliteit en reactiesnelheid als gevolg, maar verhoogt ook de kosten aangezien een groot
aantal eenheden in voorraad gehouden wordt maar de voorraadrotatie 6 laag is. Een lage product-
beschikbaarheid daarentegen verlaagt de kosten voor het aanhouden van voorraad aanzienlijk maar
heeft als belangrijk gevolg dat er aan een grotere fractie van de vraag niet kan voldaan worden. Dit
brengt dan weer andere kosten met zich mee zoals een eventueel verloren omzet (zie sectie 1.1.1.
De fundamentele trade-off bij het bepalen van de product-beschikbaarheid, en dus bij het bepalen4Bij two-part tariffs rekent de leverancier zijn volledige winst door aan de koper als een vaste kost en verkoopt de
goederen aan de productieprijs5Bij locale optimalisatie maximaliseert elke schakel in de supply chain haar eigen winst, resulterend in een lagere
winst voor de totale supply schain.6Voorraadrotatie wordt gedefinieerd als het aantal keer dat de voorraad wordt verkocht in een bepaalde periode
6

van de bestelhoeveelheid, is bijgevolg een afweging tussen de kost voor het houden van voorraad
en de kosten die plaatsvinden ten gevolge van het niet op tijd kunnen voldoen aan een gedeelte
van de vraag.
In de literatuur zijn een groot aantal verschillende classificaties van voorraad terug te vinden.
Volgens Chopra en Meindl [2, Hoofdstukken 3,10,11] kan de totale voorraad opgesplitst worden
in drie verschillende componenten die elk hun eigen trade-offs met zich meebrengen.
1. Cyclische voorraad: De gemiddelde hoeveelheid voorraad nodig om aan de vraag te vol-
doen.
2. Veiligheidsvoorraad: Voorraad die aangehouden wordt voor het geval de vraag groter is
dan verwacht.
3. Seizoensvoorraad: Voorraad die aangehouden wordt om te anticiperen op voorspelbare
fluctuaties in de vraag.
Aangezien in deze masterproef verondersteld wordt dat de tijd tussen twee opeenvolgende bestel-
lingen geometrisch verdeeld is (zie sectie 1.2) en deze verdeling niet veranderd in de tijd wordt
geen seizoensvoorraad opgenomen in het model. In hoofdstuk 3 en 4 is daarenboven ook de vei-
ligheidsvoorraad nog niet van belang. In deze twee modellen wordt immers een ’lead time’ 7 of
’levertermijn’ gelijk aan nul verondersteld en kan bijgevolg steeds voldaan worden aan de vraag.
De trade-off in deze situatie is de afweging tussen een hogere voorraadkost en een hogere bestel-
kost per eenheid, het laatste in het geval er aangekocht wordt in kleine hoeveelheden. De cyclische
voorraad die wordt aangehouden vindt zijn oorsprong in het bestaan van bepaalde schaalvoordelen
bij het kopen in grotere hoeveelheden, zoals een lagere bestelkost per eenheid. Een vaste bestel-
kost per bestelling wordt immers gespreid over een groter aantal eenheden. In hoofdstuk 5 wordt
daarentegen wel rekening gehouden met een variabele ’levertermijn’ en zal bijgevolg een veilig-
heidsvoorraad moeten aangehouden worden. Het is in dit model immers onzeker hoeveel goederen
zullen verkocht worden gedurende de tijd dat een bestelling geplaatst maar nog niet geleverd is.
De bijkomende trade-off in deze situatie bestaat uit een afweging tussen een hogere voorraadkost
en het risico dat er niet aan de vraag kan voldaan worden. Dit risico zal worden voorgesteld als de
’kost van verloren vraag’.7De lead time wordt in deze masterproef gedefinieerd als de tijd tussen het plaatsen van een bestelling en het
ontvangen van de goederen. Meer algemeen is de lead time gelijk aan de verstreken tijd tussen het begin en het eindevan een proces
7

1.1.1 Kosten verbonden aan het houden van voorraad
Zoals reeds eerder vermeld zijn er een aantal belangrijke kosten onlosmakelijk verbonden aan het
houden van voorraad en deze kostencategorie kan een aanzienlijk deel van de kostenzijde van
een onderneming innemen. In deze sectie wordt een kort overzicht gegeven van de verschillende
kosten waarmee rekening moet worden gehouden. Deze kosten kunnen evenwel in twee meer
algemene categorieen geclassificeerd worden.
De kosten verbonden aan het houden van voorraad kunnen worden opgesplitst in ’procurement-
kosten’ en ’holdingkosten’. Procurementkosten omvatten enerzijds de variabele aankoopkosten of
productiekosten en anderzijds de vaste bestelkosten of productiekosten die onafhankelijk zijn van
de hoeveelheid goederen die geproduceerd of besteld worden. Deze laatste kostencategorie omvat
onder ander de vaste kost die gepaard gaat met de administratieve afhandeling van een bestelling.
In het vervolg van deze masterproef zal deze kostencategorie voorgesteld worden door het begrip
’bestelkosten’. De holdingkosten van hun kant zijn opgebouwd uit enerzijds de opportuniteitskos-
ten van het vastgelegde kapitaal en anderzijds de kosten voor de opslag en het interne transport van
de goederen. Ook de verouderingskosten van de goederen in voorraad en de huur of aankoop van
opslagplaatsen kunnen onder deze categorie geplaatst worden. De opportuniteitskosten geven het
rendement weer dat dit kapitaal had kunnen opbrengen indien het niet in de voorraad gevangen
zat. In het vervolg van deze masterproef zal deze kostencategorie voorgesteld worden door het
begrip ’voorraadkosten’.
Paul Durlinger, een specialist in het voorraadbeheer, verdeelde de componenten die van invloed
zijn op de kosten van voorraad in drie categorieen [4]. Deze ’drie r’s’ zijn rente, ruimte en risico.
De eerste categorie, de rente, stelt hier de opportuniteitskosten van het vastgelegde kapitaal voor.
Bij dit kapitaal wordt een onderscheid gemaakt tussen eigen vermogen en vreemd vermogen. Bij
vreemd vermogen wordt over het algemeen de bankrente gebruikt als kost. Voor het eigen vermo-
gen wordt een grotere kost gerekend aangezien aandeelhouders een hoger rendement verwachten
op hun investering. Het precieze percentage dat gebruikt wordt voor deze ’rente’ is een onderwerp
van veel discussie en hangt sterk af van de aard van de onderneming. Mogelijkheden hierbij zijn
de bankrente, de Return On Investment en de hurdle rate 8. Zo zal een jong en groei-georienteerd
bedrijf een hogere kost van het eigen vermogen kennen ten opzichte van een matuur en stabiel be-
drijf [13]. Een hoger risico gaat immers altijd gepaard met een hoger verwacht rendement, hetgeen
bijgevolg gepaard gaat met een hogere opportuniteitskost van het vastgelegde kapitaal in de voor-
raad. Het meest gebruikte percentage voor het berekenen van deze kostencategorie is de gewogen
gemiddelde kosten van het vermogen of ’WACC’ 9. Deze gemiddelde kost van het vermogen van8het minimaal verwachte rendement gebruikt door ’private equity’ investeerders9Weighted average cost of capital: de voor een bedrijf gemiddelde kost van eigen en vreemd vermogen
8

een onderneming is vaak de belangrijkste factor in de totale voorraadkost [11].Deze kost varieerde
de laatste vijfentwintig jaar tussen zes en achttien procent [14].
De tweede categorie, ruimte, heeft betrekking op de ruimte die nodig is voor het opslaan van
voorraad en bevat onder andere de afschrijvingen of huur van terreinen en gebouwen, het personeel
en de aankoop van infrastructuur.
De derde categorie, risico, betreft de risico’s die het houden van voorraad met zich meebrengt,
zoals het risico dat niet verkochte voorraad verouderd geraakt, niet meer kan verkocht worden en
bijgevolg afgeschreven moet worden. In de kledij-industrie bijvoorbeeld kunnen de goederen in
voorraad met maar liefst negentig procent in waarde afnemen wanneer de mode verandert [14].
Een ander risico betreft de kans dat de goederen in voorraad in waarde verminderen. Ook het
risico op diefstal en de nodige verzekeringen die hiervoor moeten afgesloten worden kunnen onder
deze categorie ondergebracht worden. De besproken risico’s zijn uiteraard sterk afhankelijk van
de aard van de goederen in voorraad. Het risico op waardevermindering bij voedselproducten is
bijvoorbeeld veel groter dan bij duurzame goederen.
In het logistieke vakgebied wordt voor de totale kost voor het houden van voorraad vaak gebruik
gemaakt van een percentage van de totale aankoopkosten of van de waarde van de goederen in
voorraad. De vaakst gebruikte vuistregel wat betreft dit percentage is 25 procent per jaar [19], re-
kening houdend met het belastingtarief. Afhankelijk van de specifieke situatie kan dit percentage
zelfs oplopen tot 40 procent of meer. Volgens [11] schatten logistieke experts de voorraadkost
tussen 18 en 75 procent per jaar, afhankelijk van het type product en de betreffende industrietak.
Tabel 1.1 geeft de bijdrage weer van de verschillende kostencategorieen in de totale voorraadkost,
volgens [16]. Deze percentages zijn echter niet wetenschappelijk onderbouwd en zijn hoofdza-
kelijk gebaseerd op ervaring. Bovendien moet opnieuw rekening gehouden worden met het soort
goederen in voorraad. In elk geval illustreert dit hoge percentage het belang van een efficient
voorraadbeheer-beleid. Ondanks de fundamentele industriele evoluties zoals Just-In-Time, lean
manufacturing, ERP etc. blijven de voorraadkosten een belangrijk onderdeel van de kostenzijde
van een onderneming.
1.1.2 Modellen voor voorraadbeheer
Bij klassiek voorraadbeheer zal men de voorraad van een bepaald product aanvullen zodra het
voorraadniveau onder een bepaalde drempelwaarde is gezakt. Het eenvoudigste model is het Eco-
nomic Order Quantity (EOQ) model. Deze ’basis van het voorraadbeheer’ werd reeds in 1913
door Ford W. Harris [6] ontwikkeld. Met behulp van dit model kan men de bestelhoeveelheid
of productiehoeveelheid bepalen die de totale kost van het voorraadbeheer minimaliseert. Hierbij
9

Tabel 1.1: Bijdrage van diverse kostencategorieen tot de totale voorraadkost volgens Richardson (1995)
Kostencategorie % van de waarde van de goederen in voorraad
WACC 6%− 12%
Belastingen 2%− 6%
Verzekeringen 1%− 3%
Magazijnkosten 2%− 5%
Kosten voor verwerking en intern transport 2%− 5%
Controle en administratiekosten 3%− 6%
Verouderingskosten 6%− 12%
Risico op waardevermindering en diefstal 3%− 6%
Totaal 25%− 55%
wordt een afweging gemaakt tussen de bestelkosten en de voorraadkosten. Harris verwoordde dit
als volgt:
”Interest on capital tied up in wages, material and overhead sets a maximum limit to
the quantity of parts which can be profitably manufactured at one time; set-up costs
on the job fix the minimum.”
De eenvoudigste formule voor het berekenen van deze optimale of ’economische bestelhoeveel-
heid’ is de ’formule van Camp’ of de ’wet van de economische ordergrootte’ [8, Hoofdstuk 18].
Deze formule werd eveneens reeds in het begin van de twintigste eeuw ontwikkeld en is zeer be-
langrijk geweest voor de ontwikkeling van het voorraadbeheer als vakgebied. Deze wet stelt dat
we de optimale bestelhoeveelheid kunnen bepalen door de voorraadkosten af te zetten tegenover
de bestelkosten. De formule berekent de optimale trade-off tussen deze beide kosten. Indien fre-
quent en in kleine hoeveelheden besteld wordt, zal de gemiddelde bestelkost per eenheid immers
hoger zijn dan indien steeds in grote hoeveelheden wordt besteld. Het gemiddelde aantal goederen
in voorraad daarentegen zal lager zijn en bijgevolg ook de voorraadkosten. Deze afweging wordt
zichtbaar in formule (1.2) waarin de totale kost per jaar voor het houden van voorraad berekend
wordt.
TK = C0 ·D
Q+ Ch ·
Q
2+ P ·D (1.2)
De eerste term in deze formule stelt de bestelkosten voor, de tweede term de voorraadkosten
en de derde term de aankoopkosten. Deze kostencategorieen zullen allen worden opgenomen in
het model dat in deze masterproef wordt ontwikkeld. De parameters en variabelen gebruikt in
formule (1.2) en de formule van Camp worden weergegeven in tabel 1.2:
Hierbij wordt het gemiddelde aantal goederen in voorraad weergegeven door Q/2 en is D/Q
gelijk aan het aantal bestellingen per jaar. In de oorspronkelijke formule werd de voorraadkost
10

Tabel 1.2: Gebruikte parameters en variabelen in de formule van Camp
Symbool Uitleg
Q BestelhoeveelheidD Jaarlijkse vraagP Inkoopprijs van het productC0 Bestelkost per bestelling
Ch = h · P Voorraadkost per eenheidh Voorraadkost als een percentage van de prijs
Ch voorgesteld als een percentage van de prijs: h ∗ P . Zoals reeds eerder vermeld is 25% een
vaak gebruikte vuistregel. C0 is de vaste kost die gerekend wordt bij het bestellen van goederen,
onafhankelijk van de hoeveelheid. We veronderstellen hierbij dat deze kost volledig onafhanke-
lijk is van de bestelde hoeveelheid, zelfs indien deze hoeveelheid zeer groot wordt. De formule
van Camp wordt vervolgens eenvoudig afgeleid door de totale kost (formule (1.2)) te minimalise-
ren en op te lossen naar Q. De optimale bestelhoeveelheid Q∗ geeft vervolgens de economische
bestelhoeveelheid weer, zoals weergegeven in formule (1.3). Deze bestelhoeveelheid, en daaruit-
volgend de cyclische voorraad, is een resultaat van een optimale trade-off tussen de verschillende
kostencategorien.
Deze situatie wordt grafisch weergegeven in figuur 1.1. Op deze figuur wordt abstractie gemaakt
van de prijs per eenheid die betaald wordt voor het aankopen van de goederen. De formule van
Camp geeft immers duidelijk aan dat deze kost geen invloed heeft op de economische bestelhoe-
veelheid. Indien geen hoeveelheidskortingen worden gehanteerd is de aankoopkost logischerwijze
onafhankelijk van de bestelhoeveelheid.
EOQ = Q∗ =
√2 ·D · C0
Ch(1.3)
EOQ is echter een sterke vereenvoudiging van de werkelijkheid, is bijna nooit optimaal en is
bijgevolg weinig toepasbaar in een complexe bedrijfsrealiteit. Er worden namelijk een aantal
veronderstellingen gemaakt die niet altijd even realistisch zijn [18, Hoofdstuk 9]:
1. Elke bestelling wordt in een keer geleverd.
2. Elke bestelling wordt onmiddellijk geleverd. De levertermijn of lead time L is gelijk aan
nul.
3. De vraag D is deterministisch. Er is geen onzekerheid in verband met de hoeveelheid vraag
en de timing van deze vraag.
4. De vraag is vooraf bekend en constant in de tijd.
11

Bestelhoeveelheid
Kosten
EOQ
Bestelkost
V oorraadkost
Totale kost
Figuur 1.1: Relevante voorraad-gerelateerde kosten en de economische bestelhoeveelheid
5. De bestelkost C0 is constant en onafhankelijk van de grootte van de bestelling.
6. De voorraadkost per eenheid Ch is constant en onafhankelijk van het aantal goederen in
voorraad.
7. Alle goederen worden afzonderlijk geanalyseerd. Er wordt bijvoorbeeld geen rekening ge-
houden met de correlatie in de vraag naar twee substitutiegoederen. 10
8. Er zijn geen hoeveelheidskortingen of andere kortingen.
9. Eender welke discrete hoeveelheid goederen kan besteld worden.
Naarmate deze veronderstellingen minder gelden in een bepaalde situatie wordt ook de toepas-
baarheid van de formule van Camp minder groot. Het model is in zijn meest eenvoudige vorm
enkel van toepassing op de situatie afgebeeld in figuur 1.2. Op deze figuur is de situatie weergege-
ven voor twee verschillende bestelhoeveelheden Q waarbij duidelijk de invloed op de gemiddelde
voorraad en bijgevolg ook de voorraadkost blijkt. Hierbij is er bijvoorbeeld enkel sprake van
een cyclische voorraad en wordt abstractie gemaakt van een eventuele veiligheidsvoorraad en sei-
zoensvoorraad (zie sectie 1.1). Wel moet vermeld worden dat deze formule vrij robuust is. Dit wil
zeggen, indien de bestelhoeveelheid niet te veel afwijkt van de economische bestelhoeveelheid, zal
de totale kost slechts weinig veranderen. Het is dan ook vaak beter om een logistiek gezien meer
geschikte hoeveelheid te bestellen. Deze robuustheid heeft ook als gevolg dat het EOQ-model
vaak gebruikt wordt als een goede vuistregel in het voorraadbeheer. Indien voorraadkosten echter
een grote fractie van het kostenplaatje van een onderneming innemen, is het sterk aangeraden een
meer specifiek model te gebruiken. Er zijn dan ook tal van uitbreidingen in de literatuur terug
te vinden die in min of meerdere mate de dynamiek van een werkelijk voorraadbeheersysteem10Indien de vraag naar twee goederen negatief gecorreleerd is of indien deze goederen gemeenschappelijke compo-
nenten bezitten, is het voordelig om de voorraadbeslissingen gezamenlijk te nemen (omwille van ’variability pooling’).
12

kunnen vatten. De literatuur in dit vakgebied is voornamelijk deterministisch.
t
V oorraadniveau
Q
Q/2
Q/D
slope = D
Figuur 1.2: Evolutie in de tijd van het voorraadniveau met de formule van Camp
In de literatuur zijn tal van versoepelingen terug te vinden ten opzichte van de veronderstellingen
die inherent in het EOQ model aanwezig zijn. Wanneer bijvoorbeeld de tweede veronderstelling
versoepeld wordt en een constante levertermijn of lead time τ verondersteld wordt, verkrijgen
we de situatie zoals weergegeven in figuur 1.3. In plaats van te bestellen op het moment dat
de voorraad uitgeput is, zal nu reeds vroeger besteld worden, namelijk op het ’reorder point’ of
bestelpunt. Dit moment in de tijd komt overeen met een welbepaald voorraadniveau, het ’reorder
level’ of bestelniveau. De veiligheidsvoorraad wordt vervolgens eenvoudig berekend met behulp
van formule (1.4). Hierbij stelt L de levertgermijn voor.
V eiligheidsvoorraad = Bestelniveau−D ∗ L (1.4)
t
V oorraadniveau
Lead time
Bestelniveau
Bestelpunt
Figuur 1.3: Evolutie van de voorraad in de tijd met constante levertermijn en deterministische vraag
Een tweede uitbreiding van het EOQ model die leidt tot een betere benadering van de werkelijk-
heid is het veronderstellen van een variabele, stochastische vraag in tegenstelling tot een determi-
13

nistische vraag. Omdat de vraag in deze situatie onzeker is en indien een levertermijn groter dan
nul wordt verondersteld, zal een veiligheidsvoorraad worden aangelegd. Hierdoor zal de kans dat
niet aan de vraag kan voldaan worden kleiner worden. Indien de levertermijn stochastisch is in
plaats van de vraag, zal eveneens een veiligheidsvoorraad moeten aangelegd worden. Deze vorm
van onzekerheid situeert zich aan de aanbodzijde. Deze situatie wordt weergegeven in figuur 1.4,
waarbij de levertermijn voorgesteld wordt door τ . Indien zowel de vraag als de levertermijn sto-
chastisch zijn of als de onzekerheid groter wordt, dan zal de veiligheidsvoorraad ook groter moeten
zijn om een welbepaalde service level te behalen. De kansverdeling van de vraag gedurende de
levertermijn wordt immers gegeven door de convolutie (het ’optellen’) van de kansverdeling van
de vraag per tijdseenheid en de kansverdeling van de levertermijn [2]. De situatie weergegeven in
figuur 1.4 met fluctuerende vraag en stochastische levertermijn is gelijkaardig aan het meer realis-
tische model dat ontwikkeld wordt in hoofdstuk 5. In dit model zal de tijd tussen 2 opeenvolgende
bestellingen echter niet willekeurig en continu zijn zoals in figuur 1.4, maar zal deze geometrisch
verdeeld en bijgevolg discreet zijn. Dit wil zeggen dat op elk tijdstip de vraag zal gelijk zijn aan
een of afwezig zal zijn, afhankelijk van een bepaalde kans op vraag p.
t
V oorraadniveau
τ1 τ2 Onzekere toekomst
Gemiddeldevoorraad
t0
Bestelniveau
V eiligheidsvoorraad
Cyclischevoorraad
Q
1
Figuur 1.4: Evolutie van de voorraad in de tijd met stochastische vraag en lead time
In de bovenstaande modellen wordt steeds verondersteld dat de voorraad continu gecontroleerd
wordt en er besteld wordt van zodra het voorraadniveau een bepaalde drempelwaarde bereikt.
Bij deze ’continue voorraadbeheer-systemen’ is er een vaste bestelhoeveelheid maar varieert het
tijdsinterval tussen twee opeenvolgende bestellingen. Er bestaan echter ook modellen waarbij
het dit tijdsinterval vastligt, bijvoorbeeld dagelijks, en ook het maximale voorraadniveau vastligt,
maar waarbij de bestelhoeveelheid varieert. Deze modellen worden geclassificeerd als ’periodieke
voorraadbeheer-systemen’ [2]. Het model in deze masterproef valt strikt gezien onder de continue
voorraadbeheer-systemen aangezien er op elk tijdstip een beslissing wordt genomen in verband
14

met het bestellen van goederen. In tegenstelling tot de uitbreidingen van het EOQ-model zoals
beschreven in deze sectie, wordt er echter niet gewerkt met een vaste bestelhoeveelheid maar
hangt deze af van de eenheidsprijs op dat specifieke tijdstip. Dit onderscheid zal belangrijk zijn
wanneer in hoofdstuk 2 de methodiek gekozen wordt voor het modelleren van de probleemstelling
van deze masterproef.
1.2 Specifieke uitdagingen
Het EOQ voorraadmodel veronderstelt een constante, deterministische vraag en een vaste aan-
koopprijs, alsook een levertermijn gelijk aan nul. Het gebruik van dit klassieke model in een
dynamische omgeving levert, ondanks de robuustheid van het model, dan ook weinig accurate
resultaten op. De concrete uitdaging die in deze masterproef wordt aangegaan is het integreren
van marktfluctuaties in een wiskundig model. Meer specifiek wordt een voorraadmodel ontwor-
pen met betrekking tot goederen die gekenmerkt worden door twee soorten marktfluctuaties. Ten
eerste is dit de fluctuatie van de prijs rond een lange-termijn gemiddelde. Ten tweede worden
vraagfluctuaties in het model opgenomen. Dit laatste gebeurt door middel van de geometrische
verdeling, zoals reeds eerder aangehaald.
De invloed van vraagfluctuaties is reeds uitgebreid onderzocht als een uitbreiding van het klassieke
EOQ-model, bijvoorbeeld in het Wilson EOQ-model [9]. K. Yan and V. Kulkarni [12] hebben een
voorraadsysteem ontwikkeld waarbij de stochastische vraag gemodelleerd wordt aan de hand van
een continue-tijd Markov-keten (zie hoofdstuk 2). Hierbij worden echter enkele vereenvoudigende
veronderstellingen gemaakt zoals een levertermijn gelijk aan nul en de beperking dat enkel kan
besteld worden als de voorraad uitgeput is. Deze situatie is vergelijkbaar met het eenvoudige
model uit hoofdstuk 3 met als belangrijk verschil dat hier zal gewerkt worden met een discrete-tijd
Markov-keten. Beide vereenvoudigende veronderstellingen in [12] worden vervolgens weggelaten
in hoofdstukken 4 en 5, hetgeen leidt tot een meer realistisch model. In figuur 1.4 werd deze
situatie reeds voorgesteld, weliswaar met een willekeurige, continue vraag terwijl de vraag in deze
masterproef discreet is.
In tegenstelling tot vraagfluctuaties is de invloed van prijsfluctuaties nog een wetenschappelijk
weinig ontgonnen terrein. Jinn-Tsair Teng et al. [22] hebben een algoritme opgesteld dat naast
een veranderende vraag ook een veranderende prijs veronderstelt, maar dit algoritme heeft betrek-
king op een continue lange-termijn prijsdaling, wat bijvoorbeeld in de IT sector vaak het geval is.
Het opnemen van prijsfluctuaties in het model zal de beslissing om een bepaalde hoeveelheid te
bestellen niet langer laten afhangen van enkel het voorraadniveau, ook het prijsniveau wordt nu
belangrijk. De mogelijkheid om aan een relatief goedkope prijs aan te kopen weegt mogelijk op
15

tegen een hogere ’holding-kost’ of voorraadkost. Dit impliceert dat bij iedere mogelijke combi-
natie van prijs- en voorraadniveau een beslissing moet worden genomen over enerzijds het al dan
niet bestellen en anderzijds de bestelhoeveelheid.
Ter verduidelijking, onder de term fluctuaties bedoelen we in deze masterproef korte-termijn fluc-
tuaties rond een lange-termijn gemiddelde. Het model is dus niet van toepassing op continu in
prijs dalende of stijgende goederen, zoals bijvoorbeeld hightech producten in de IT sector. Lange-
termijn-fluctuaties (conjunctuur) vallen eveneens buiten het bereik van het model. Wat betreft de
vraagfluctuaties is dit model hoofdzakelijk van toepassing op producten in de maturiteitsfase waar
de gemiddelde vraag als constant kan worden verondersteld. De vraagfluctuaties situeren zich dan
rond dit lange-termijn gemiddelde. Dit wordt zoals reeds eerder vermeld voorgesteld met behulp
van de geometrische verdeling. Een belangrijk gevolg van de veronderstelling dat de markt op
lange termijn stabiel blijft, is dat er kan gewerkt worden met een stationaire Markov-keten (zie
hoofdstuk 2).
16

Hoofdstuk 2
Onderzoeksaanpak
In hoofdstuk 1 werd reeds besproken in welke bedrijfsspecifieke omgeving het model in deze
masterproef van toepassing is, of kan zijn mits kleine aanpassingen afhankelijk van de veronder-
stellingen die gemaakt moeten worden. In dit hoofdstuk wordt de wiskundige theorie uiteengezet
waarmee dit probleem zal gemodelleerd en opgelost worden.
2.1 Methodologie
In deze masterproef zal de dynamiek van het voorraadbeheer beschreven worden aan de hand van
twee Markov-ketens. Met behulp van de theorie van Markoviaanse beslissingsprocessen kan dan
een optimaal prijsafhankelijk voorraadbeheer bepaald worden. Het uiteindelijke doel is dus het
optimale bestelbeleid te bepalen die in elke toestand van het systeem aangeeft of en hoeveel er
moet besteld worden.
In secties 2.1.1 en 2.1.3 wordt een korte theoretische uiteenzetting gegeven over de wiskundige
modelleringstechnieken die in deze masterproef zullen worden gebruikt. In sectie 2.1.2 wordt
verder ingegaan op de eigenschappen van Markov-ketens. Bij het opstellen van de verschillende
modellen in hoofdstukken 3, 4 en 5 zal meer uitgebreid aangegeven worden hoe deze theoretische
concepten concreet zijn toegepast in deze masterproef. In sectie 2.2 worden enkele veel gebruikte
methodes besproken die kunnen gebruikt worden om een Markoviaans beslissingsproces op te
lossen. In sectie 2.3 ten slotte wordt aangegeven hoe de theorie in dit hoofdstuk gebruikt zal
worden voor het behandelen van de probleemstelling besproken in hoofdstuk 1.
2.1.1 Markov-ketens
Deze sectie is geschreven op basis van de omschrijvingen en definities in [8, Hoofdstuk 16], [23],
[20] en [3].
17

De meeste optimalisatieproblemen zijn in de praktijk stochastisch van aard, ook in het domein
van het voorraadbeheer. Dit houdt in dat dergelijke systemen inherent bepaalde onzekerheden
in zich hebben, zoals bijvoorbeeld de hoeveelheid vraag of de prijs op een bepaald tijdstip. Op
het moment dat men een bepaalde beslissing moet nemen, zoals het plaatsen van een bestelling,
beschikt men met andere woorden nog niet over alle relevante en noodzakelijke informatie.
Een Markov-keten is een specifieke vorm van een stochastisch proces; het kan eenvoudig be-
schreven worden als een proces dat op probabilistische wijze evolueert in de tijd en hierbij door
een aantal toestanden beweegt. Een stochastisch proces wordt gedefinieerd als een geındexeerde
verzameling van toevalsvariabelen {Si} = {S0, S1, S2, . . .}, waarbij de index i een element is
van een gegeven verzameling I . In het specifieke geval van deze thesis worden respectievelijk het
voorraadniveau en de aankoopprijs voorgesteld door een dergelijke grootheid, gemeten op discrete
tijdstippen t. Een stochastisch proces kan gebruikt worden voor het beschrijven van het gedrag
van een systeem dat evolueert in de tijd, waarbij het systeem zich in een verzameling mutueel
exclusieve toestanden Si kan bevinden. De toestand van het systeem wordt vervolgens geobser-
veerd op discrete tijdstippen t. St stelt dan de toestand van het systeem voor op tijdstip t, in dit
specifieke geval het voorraad- en prijsniveau op tijdstip t.
Om deze stochastische processen analytisch te kunnen bestuderen zijn echter veronderstellingen
nodig inzake de gezamenlijke verdeling van {St}. Een Markov-keten is een voorbeeld waarbij een
dergelijke veronderstelling gemaakt wordt. Een Markov-keten is namelijk een stochastisch proces
dat voldoet aan de ’Markoviaanse eigenschap’. Deze eigenschap vertelt ons dat bij Markov-ketens
de voorwaardelijke probabiliteiten of kansen inzake de toekomstige evolutie van het proces enkel
afhankelijk zijn van de huidige toestand van het proces en dus onafhankelijk zijn van gebeurte-
nissen of toestanden in het verleden. In wiskundige termen wordt dit: een stochastisch proces Stvoldoet aan de Markoviaanse eigenschap indien:
Pr{St+1 = j|S0 = k0, S1 = k1, . . . , St−1 = kt−1, St = i} = Pr{St+1 = j|St = i}, (2.1)
met t = 0, 1, . . .
Voor het verdere verloop van deze masterproef zullen steeds discrete tijdsintervallen verondersteld
worden. We hebben dus te maken met een ’discrete-tijd-Markov-keten’, waarbij de toestand van
het systeem slechts geobserveerd wordt op discrete tijdstippen in tegenstelling tot het continu ob-
serveren. Dit verschil is vanzelfsprekend te verwaarlozen indien deze tijdsintervallen klein genoeg
gekozen worden. De keuze voor een discrete-tijd-Markov-keten vereenvoudigt de berekeningen
echter aanzienlijk.
18

Gegeven de huidige toestand van het systeem worden de kansen voor de overgang naar de vol-
gende toestand gegeven door een een-staps ’overgangsmatrix’ of ’transitiematrix’. De elementen
van deze transitiematrix zijn de voorwaardelijke kansen pij = Pr{St+1 = j|St = i}. Deze
worden ’overgangskansen’ of ’transition probabilities’ genoemd. Deze transitiematrices hebben
enkele belangrijke en karakteristieke eigenschappen. In elke rijvector zijn alle waarden name-
lijk positief en is hun som gelijk aan een. Dergelijke vectoren worden ’kansvectoren’ genoemd.
Een matrix waarbij alle rijvectoren kansvectoren zijn wordt een transitiematrix of stochastische
matrix genoemd. Andrei Markov, een Russische wiskundige, was de eerste wiskundige die der-
gelijke matrices onderzocht. In het begin van de 20ste eeuw ontwikkelde hij op basis hiervan de
fundamenten van de Markov-keten theorie.
Een belangrijke veronderstelling in deze masterproef is dat alle overgangskansen ’stationair’ zijn.
Men zegt dat deze overgangskansen pij stationair zijn indien deze niet veranderen in de tijd, of
met andere woorden indien:
∀i, j : Pr{St+1 = j|St = i} = Pr{S1 = j|S0 = i},∀t = 1, 2, . . . (2.2)
Of ook:
∀i, j : Pr{St+n = j|St = i} = Pr{Sn = j|S0 = i},∀t = 1, 2, . . . (2.3)
In dit geval wordt ook gesproken over een stationaire Markov-keten.
2.1.2 Lange-termijn eigenschappen van een Markov-keten
Een een-staps transitiematrix geeft ons een eenvoudig beeld van de evolutie van het systeem op
korte termijn. Het is echter vaak interessanter om de evolutie op langere termijn te bekijken.
Hiervoor worden de ’n-staps overgangskansen’ gebruikt. Deze worden gedefinieerd als:
p(n)ij = Pr{St+n = j|St = i}. (2.4)
Het bestaan van stationaire overgangskansen heeft als gevolg dat de kansen p(n)ij gegeven worden
door vergelijking (2.3). p(n)ij is met andere woorden de kans dat het systeem zich in toestand j
zal bevinden na exact n tijdseenheden, gegeven dat het systeem zich in toestand i bevindt. De
’Chapman-Kolmogorov vergelijkingen’ leiden tot een eenvoudige methode voor het berekenen
van p(n)ij [8, Hoofdstuk 16]. Uit deze vergelijkingen volgt dat de n-staps transitiematrices P(n)
eenvoudig kunnen berekend worden als zijnde de n-de macht van de een-staps transitiematrix P:
19

P(n) = Pn (2.5)
Onder bepaalde voorwaarden kan een Markov-keten na verloop van tijd convergeren naar de zoge-
naamde ’steady-state kansen’ die de kans weergeven dat het systeem zich in een bepaalde toestand
bevindt, onafhankelijk van de initiele toestand. Voor elke irreducibele 1, ergodische Markov-
keten 2 geldt immers dat limn→∞ p(n)ij bestaat en onafhankelijk is van de initiele toestand i of Si.
Dit wordt wiskundig weergegeven door vergelijking (2.6) [8, Hoofdstuk 16].
limn→∞
p(n)ij = πj > 0 (2.6)
Hierbij stellen πj de unieke oplossing voor van de ’steady-state’ vergelijkingen (2.7) en (2.8).
M∑i=0
(πi · pij) = πj (2.7)
met j = 0, 1, . . . ,M
M∑j=0
πj = 1 (2.8)
In matrixvorm wordt vergelijking (2.7):
π = π ·P (2.9)
met π = (π0, π1, . . . , πM ).
Deze steady-state kansen zullen belangrijk zijn bij het modelleren van de prijsfluctuaties later in
deze masterproef (zie sectie 3.2.2). Met behulp van deze theorie kan namelijk het gemiddelde
prijsniveau van een Markov-keten berekend worden, alsook de volledige lange-termijn kansver-
deling van dit prijsniveau.
2.1.3 Markoviaanse beslissingsprocessen
Deze sectie is geschreven op basis van de omschrijvingen en definities in [23], [8, Hoofdstuk 19]
en [20].1Een Markov-keten is irreducibel indien vanuit elke toestand alle mogelijke toestanden kunnen bereikt worden in
een eindig aantal stappen2zie [8, Hoofdstuk 16]
20

Vele belangrijke systemen kunnen gemodelleerd worden door middel van een Markov-keten. Het
is uitermate nuttig het gedrag van een dergelijk systeem te beschrijven om zodoende de prestaties
ervan te evalueren. We kunnen echter nog een stap verder gaan door de werking van het sys-
teem aan te passen om op deze manier de prestaties te optimaliseren. In plaats van het ontwerp
van de Markov-keten en de bijbehorende overgangsmatrix en verwachte evolutie van het systeem
passief over te nemen, kan ook proactief gewerkt worden. In dit opzicht hebben we te maken
met stochastische optimalisatieproblemen waarin, op specifieke momenten in de tijd, beslissingen
kunnen genomen worden om het systeem te sturen. Markoviaanse beslissingsprocessen vormen
een raamwerk voor het modelleren van dergelijke problemen.
Bij Markoviaanse beslissingsprocessen wordt bij elke mogelijke toestand van de Markov-keten een
beslissing genomen over het ondernemen van een bepaalde actie, genomen uit een verzameling
van mogelijke acties. De actie die gekozen wordt heeft een invloed op zowel de overgangskan-
sen als op de onmiddellijke en toekomstige kosten (of beloningen). Het doel is vervolgens het
vinden van de optimale actie in elke toestand om zodoende deze kosten (of beloningen) te mini-
maliseren (respectievelijk maximaliseren). Het beslissingsproces dat hiermee gepaard gaat wordt
een Markoviaans beslissingsproces genoemd. Deze processen werden reeds beschreven door R.
Bellman in 1957 [1]. De toepassingen in de praktijk zijn talrijk; Markoviaanse beslissingspro-
cessen worden onder andere gebruikt in artificiele intelligentie, robottechnologie, automatisatie,
economie en wiskunde.
Markoviaanse beslissingsprocessen verschaffen ons bijgevolg een wiskundig kader voor het mo-
delleren van systemen die deels op toeval berusten en deels gecontroleerd kunnen worden door
een beslissingsnemer. De beslissingen hebben niet alleen invloed op de toestand van het sys-
teem op dit moment, maar ook op het gedrag van het systeem in de toekomst. Dit concept is
de sleutel voor een veel gebruikte oplossingsmethode, namelijk het dynamisch programmeren.
Markov-beslissingsprocessen kunnen echter ook opgelost worden via lineair programmeren. Vaak
gebruikte oplossingsmethodes die gebaseerd zijn op het dynamisch programmeren zijn ’value ite-
ration’ en ’policy iteration’ (zie sectie 2.2).
Hieronder wordt het model besproken dat gebruikt werd door F. Hillier & G. Lieberman (2010) [8,
Hoofdstuk 19]. Dit model lijkt uitermate geschikt als basis voor het vervolg van deze masterproef.
In onderstaande beschrijving wordt φ gebruikt als symbool voor het bestelbeleid, in tegenstelling
tot de gangbare literatuur waar over het algemeen π gebruikt wordt als symbool. De reden hiervoor
is het vermijden van verwarring met het symbool π in sectie 2.1.2.
1. toestand Si van een discrete-tijd-Markov-keten wordt geobserveerd op elk discreet tijdstip
(i = 0, 1, . . . ,M ).
21

2. Na elke observatie wordt voor elke toestand Si een beslissing of actie di gekozen uit een ver-
zameling van K beslissingsmogelijkheden (k = 1, 2, . . . ,K). Het is mogelijk dat bepaalde
beslissingen niet relevant zijn voor bepaalde toestanden.
3. Indien een beslissing di = k genomen wordt in toestand i, dan gaat hiermee een kost Cikgepaard.
4. De beslissing di = k beınvloedt de overgangskansen pij(k) voor de overgang van de huidige
toestand i naar de volgende toestand.
5. Het vastleggen van een beslissing di (i = 0, 1, . . . ,M ) in elke mogelijke toestand resul-
teert in een beleid of ’policy’ Φ voor de desbetreffende Markov-keten. Dit beleid geeft de
optimale actie φi weer in elke mogelijke toestand i.
6. Het doel is vervolgens het vinden van een optimaal beleid dat zowel de onmiddellijke als
toekomstige kosten in rekening neemt. Een veelgebruikt kostencriterium hierbij is het mi-
nimaliseren van de (lange-termijn) verwachte gemiddelde kost per tijdseenheid. Een andere
mogelijkheid is het minimaliseren van de verwachte totale verdisconteerde kost met dis-
conteringsfactor r. Beide criteria zijn geschikt voor ons opzet aangezien we werken met
een oneindige horizon. In het vervolg van deze masterproef zal steeds de verdisconteerde
kost geminimaliseerd worden (zie formule (2.10)). In sectie 2.3 wordt de motivatie hiervoor
uiteengezet.
∞∑t=0
γtCikt , γ =1
1 + r, 0 < γ ≤ 1 (2.10)
Hierbij stelt r de huidige interestvoet voor. γt is bijgevolg gelijk aan de huidige waarde van een
kost-eenheid, t tijdsperiodes in de toekomst.
Dit algemene model is een Markoviaans beslissingsproces want het bezit de Markoviaanse ei-
genschap waaraan elk Markov-proces moet voldoen. Er is hier aan de Markoviaanse eigenschap
voldaan aangezien:
1. We te maken hebben met een Markov-keten.
2. Nieuwe overgangskansen enkel afhankelijk zijn van de huidige toestand en de beslissing.
3. De onmiddellijke verwachte kost eveneens enkel afhankelijk is van de huidige toestand en
de beslissing.
De bovenvermelde beschrijving van een beleid heeft twee belangrijke gevolgen die verondersteld
zullen worden doorheen de volledige masterproef. Een eerste eigenschap die eruit volgt is dat een
22

beleid ’stationair’ is; dit wil zeggen, als een systeem zich in toestand i bevindt zal de beslissing
steeds dezelfde zijn, onafhankelijk van het tijdstip t. De tweede eigenschap zegt dat een beleid
deterministisch is; dit wil zeggen, als een systeem zich in toestand i bevindt zal er steeds een
welbepaalde beslissing genomen worden. Dit in tegenstelling tot een ’gerandomiseerd beleid’
waar een kansverdeling gebruikt wordt voor het selecteren van een beslissing. Als gevolg van
deze twee eigenschappen hebben we te maken met een stationair, deterministisch beleid.
Het resultaat van het vooropgesteld model zal bijgevolg een eenvoudige tabel zijn die een opti-
male actie toewijst aan elke mogelijke toestand. Met andere woorden, bij elke combinatie van
voorraad- en prijsniveau zal een beslissing vastgelegd worden omtrent de te bestellen hoeveel-
heid goederen en dit bestelbeleid is onafhankelijk van de tijd. Het beleid is optimaal indien de
verwachte verdisconteerde of gemiddelde kost minimaal is.
2.2 Oplossingsmethodes
Beknopt kunnen we de vorige secties samenvatten door te stellen dat een Markoviaans beslissings-
proces zeer gelijkaardig is aan een Markov-keten in de zin dat in beide de evolutie van een systeem
beschreven wordt als een reeks overgangen tussen een verzameling voorgedefinieerde toestanden.
Een Markoviaans beslissingsproces verschilt echter van een Markov-keten in de zin dat de transi-
tiematrix nu afhankelijk is van de actie die ondernomen wordt door de beslissingsnemer. Aan elke
combinatie van toestand en actie is een kost verbonden. Het doel is vervolgens het vinden van
een optimaal beleid waarin gespecificeerd wordt welke actie genomen moet worden in elke moge-
lijke toestand teneinde de totale verdisconteerde of gemiddelde kost te minimaliseren. De meest
gebruikte oplossingsmethodes voor dit probleem zijn value iteration en policy iteration. Deze
zullen in deze sectie kort besproken worden, samen met een aantal andere maar vaak minder ef-
ficiente oplossingsmethodes. Belangrijk is om te vermelden dat de formules en algoritmes in deze
sectie enkel gelden indien de totale verdisconteerde kost gebruikt wordt als kostencriterium en
niet de gemiddelde kost. De transitiematrix en kostmatrix worden gedefinieerd in formules (2.11)
en (2.12):
Pa(s, s′) = Pr{St+1 = s′|St = s, dt = a} (2.11)
Ra(s, s′) = E[Rt+1|St = s, St+1 = s′, dt = a] (2.12)
Hierbij stelt ’E’ het symbool voor voor de verwachte waarde. De transitiematrix Pa(s, s′) geeft de
kansen weer dat een systeem dat zich in toestand s of St (rij-variabelen) bevindt op tijdstip t, zich
in toestand s′ of St+1 (kolom-variabelen) zal bevinden op tijdstip t + 1, indien actie a gekozen
wordt. Voor elke mogelijke actie a bestaat er met andere woorden een andere twee-dimensionale
23

transitiematrix P (s, s′). Een illustratie van een dergelijke transitiematrix is hieronder weergege-
ven. Hierbij stellen ai, bi, ci, di en ei de overgangskansen voor.
St | St+1 S1 S2 S3 S4 S5
S1 a1 a2 a3 a4 a5
S2 b1 b2 b3 b4 b5
S3 c1 c2 c3 c4 c5
S4 d1 d2 d3 d4 d5
S5 e1 e2 e3 e4 e5
De kostmatrix Ra(s, s′) stelt op haar beurt de kost voor die verbonden is aan een evolutie van
het systeem van toestand s naar toestand s′ op het volgende tijdstip, gegeven dat actie a gekozen
werd. Vaak is deze kost onafhankelijk van de toestand s′ waarin het systeem zal terechtkomen.
Met andere woorden:
Ra(s, s′) = Ra(s) = E[Rt+1|St = s, dt = a] (2.13)
Deze vereenvoudiging zal ook toepasbaar zijn op het model in deze masterproef, aangezien ener-
zijds de bestelkost enkel afhankelijk is van de huidige prijs en de bestelhoeveelheid en anderzijds
de voorraadkost enkel afhankelijk is van het huidige voorraadniveau. In welke toestand het sys-
teem terechtkomt op het volgende tijdstip, afhankelijk van eventuele vraag en prijswijzigingen, is
bijgevolg irrelevant voor het berekenen van de kost.
Alhoewel het in theorie mogelijk is een Markoviaans beslissingsproces op te lossen door middel
van het berekenen van de totale kost voor elk mogelijk beleid, is dit praktisch onmogelijk voor
grotere problemen. Meerdere algoritmes zijn evenwel voorhanden om het optimale bestelbeleid
op een meer efficiente wijze te vinden. In deze masterproef zullen 5 verschillende oplossings-
methodes worden gebruikt en vergeleken teneinde de meest efficiente methode te vinden voor dit
specifieke model. Deze methodes zijn het lineair programmeren, ’policy iteration’, ’value itera-
tion’ en een aangepast algoritme van zowel policy als value iteration. Lineair programmeren buiten
beschouwing gelaten zijn deze oplossingsmethodes allen zeer gelijkaardig en maken ze gebruik
van dezelfde vergelijkingen als basis. De onderstaande paragrafen zijn hoofdzakelijk gebaseerd
op [8, Hoofdstuk 19], [23] en [20].
Bij het oplossen van een Markoviaans beslissingsproces zijn twee functies van groot belang die
iteratief worden opgelost voor elke toestand s. Ten eerste is dit het beleid φ(s) voor elke toestand
s. Dit stelt dus de bestelhoeveelheid voor indien het systeem zich in toestand s bevindt. Ten
tweede wordt een nieuwe variabele ingevoerd, namelijk de ’waarde’ van een bepaalde toestand s
24

indien een welbepaald beleid φ gevolgd wordt. Deze waarde wordt weergegeven als V φ(s). Deze
vergelijking kan opgesteld worden voor elke toestand s hetgeen leidt tot een stelsel vergelijkingen.
Het oplossen van dit stelsel wordt ’value determination’ of ’waardebepaling’ genoemd. Het op-
timale beleid, genoteerd als φ∗, is vervolgens het beleid waarbij de waarden V φ(s) groter dan of
gelijk zijn aan elk ander bestelbeleid in elke mogelijke toestand s. Een groot aantal oplossingsme-
thodes, zoals policy iteration en value iteration, kunnen gezien worden als een iteratieve interactie
tussen deze twee reeksen, weergegeven in formules (2.14) en (2.15)3 [20]. Deze formules moeten
berekend worden voor elke mogelijke toestand s. Hierbij stelt k de opeenvolgende iteraties voor.
k + 1 is met andere woorden een indicatie voor de volgende iteratie.
φ(s) = arg maxa
{∑s′
Pa(s, s′) ·(Ra(s, s
′) + γ · V (s′))}
(2.14)
Vk+1(s) =∑s′
Pφ(s)(s, s′) ·(Rφ(s)(s, s
′) + γ · Vk(s′))
(2.15)
Hierbij is de waarde-functie V (s) de verwachte totale verdisconteerde kost wanneer het systeem
vertrekt in toestand s, beleid φ wordt toegepast en wanneer dit systeem evolueert tot in het onein-
dige. Formule 2.15 bevat op zich evenveel vergelijkingen als er toestanden zijn en tevens evenveel
onbekenden. V (s) wordt bijgevolg gevonden door het oplossen van dit stelsel vergelijkingen.
Een aantal verschillende algoritmes maken gebruik van deze twee stappen. De volgorde waarin
deze stappen uitgevoerd worden hangt echter af van de specifieke variant of algoritme. Bij som-
mige algoritmes worden bovendien bovenstaande vergelijkingen opgelost voor alle toestanden
samen of een voor een. Echter, zolang geen enkele toestand systematisch wordt uitgesloten zal
uiteindelijk de optimale oplossing bereikt worden.
2.2.1 Lineair programmeren
Ten eerste is het mogelijk een Markoviaans beslissingsproces op te lossen met behulp van het
lineair programmeren, de meest gebruikte optimalisatiemethode. Deze methode gebruikt een ma-
thematisch model voor het beschrijven van een probleem. ’Lineair’ betekent dat alle wiskundige
functies in het model verplicht lineaire functies moeten zijn 4. Lineair programmeren kan eenvou-
dig omschreven worden als het plannen van acties om een optimaal resultaat te bereiken, rekening
houdend met alle realiseerbare alternatieven. De methode wordt hoofdzakelijk gebruikt voor het
toewijzen van schaarse goederen aan een aantal concurrerende activiteiten en dit op een optimale
wijze. In deze masterproef houdt dit in dat op elk tijdstip een optimale beslissing genomen wordt3argmaxa f(x) stelt het argument van het maximum voor. Met andere woorden, dit is de verzameling van waarden
voor a waarvoor de functie f(x) haar maximale waarde bereikt.4Een lineaire functie is een functie van de vorm a · x+ b, waarin a en b constanten zijn.
25

omtrent de bestelhoeveelheid.
Een Markoviaans beslissingsproces kan enkel worden geformuleerd als een lineair programmerings-
probleem indien initieel verondersteld wordt dat een beleid niet deterministisch maar gerandomi-
seerd is. Dit is noodzakelijk opdat het model zou kunnen opgelost worden met behulp van de
simplex-methode, het bekendste algoritme om dergelijke problemen op te lossen. De oplossing
zal evenwel steeds deterministisch zijn en bijgevolg kan het lineair programmeren gebruikt worden
voor het vinden van een optimaal, deterministisch beleid (zie ook sectie 2.1.3) zoals in deze mas-
terproef. De precieze formulering van een Markoviaans beslissingsproces als een lineair probleem
is terug te vinden in [8, Hoofdstuk 19].
2.2.2 Policy iteration
Naast het lineair programmeren kunnen Markoviaanse beslissingsprocessen ook opgelost worden
met behulp van het dynamisch programmeren. In de volgende paragrafen worden hiervan enkele
vaak gebruikte varianten beschreven. Een tweede populaire oplossingsmethode is het ’policy im-
provement algoritme’ of ’policy iteration’, waarbij het beleid iteratief verbeterd wordt. [10]. Het
grootste voordeel van deze methode is haar grote efficientie. De optimale oplossing wordt immers
bereikt na een veel kleiner aantal iteraties in vergelijking met het simplex algoritme bij het lineair
programmeren. De eerste stap in dit algoritme is het kiezen van een willekeurig beleid φ1. Er
wordt met andere woorden een willekeurige actie di gekozen voor elke toestand si.
Vervolgens wordt in de ’waardebepaling’- (of ’beleidsevaluatie’-)stap een reeks vergelijkingen op-
gelost voor elke toestand s zoals in formule (2.15). Voor elke toestand swordt met andere woorden
een waarde V1(s) berekend. Op basis van dit resultaat wordt dan in de ’beleidsverbetering’-stap
een verbeterd beleid φ2 opgesteld zoals in formule (2.14). Dit proces komt overeen met een ite-
ratie. Hierna worden opnieuw de vergelijkingen V2(s) van de waardebepaling-stap opgesteld en
uitgewerkt, waarna opnieuw een verbeterd beleid φ3 wordt opgesteld. Dit iteratieve proces wordt
herhaald tot twee opeenvolgende iteraties een identiek beleid opleveren. Dit beleid φ∗ is het opti-
male (bestel)beleid:
φ0E
GGGGGAV φ0I
GGGGAφ1E
GGGGGAV φ1I
GGGGAφ2E
GGGGGA . . .I
GGGGAφ∗E
GGGGGAV ∗
Hierbij steltE
GGGGGA de beleidsevaluatie-stap voor terwijl de beleidsverbetering-stap wordt weerge-
geven doorI
GGGGA. Figuur 2.1 [20] geeft de interactie tussen het beleid en de waarde-functie gra-
fisch weer. Een groot voordeel van deze oplossingsmethode is de aanwezigheid van een duidelijk
stopcriterium: het algoritme is voltooid indien φ niet wijzigt bij het toepassen van formule (2.14)
26

(beleidsverbetering-stap). Bovendien garandeert dit algoritme een optimale oplossing in een ein-
dig aantal iteraties aangezien ook het aantal mogelijkheden voor het bestelbeleid eindig is. Merk
ook op dat elke beleidsevaluatie Vk+1(s), op zich ook een iteratief proces, vertrekt van de waar-
defunctie Vk(s′) van het beleid uit de vorige iteratie. Over het algemeen levert dit een grotere
convergentiesnelheid op. Een meer gedetailleerde weergave van dit algoritme is neergeschreven
in [8, Hoofdstuk 19] en [21] en [23].
φ V
Waardebepaling
V → V φ
Beleids− verbetering
φ→ φ′
φ∗ V ∗
...
Figuur 2.1: In het policy iteration algoritme voor het oplossen van Markoviaanse beslissingsprocessen iser een continue interactie tussen beleids- en waardefuncties die stopt wanneer hun optimalewaardes bereikt worden [20]
2.2.3 Modified policy iteration
’Modified policy iteration’ is, zoals de naam al aangeeft, een licht aangepaste versie van het policy
iteration algoritme. Ook in dit algoritme wordt het bestelbeleid immers iteratief verbeterd. Bij het
standaard policy iteration algoritme wordt de eerste stap (beleidsverbetering) per iteratie eenmaal
uitgevoerd, terwijl de tweede stap (beleidsevaluatie) herhaald wordt tot ze convergeert. Een an-
dere, meer efficiente mogelijkheid voor het oplossen van deze tweede stap is het oplossen ervan
als een stelsel lineaire vergelijkingen (een vergelijking voor elke toestand).
In deze aangepaste versie wordt de tweede, beleidsevaluatie-stap echter slechts een beperkt aantal
keer herhaald en niet tot er convergentie optreedt. Bovendien is bij deze variant het algoritme
voltooid indien een epsilon-optimale oplossing wordt gevonden in tegenstelling tot het oorspron-
kelijke algoritme waar er een strikt stopcriterium is voor optimaliteit [15].
2.2.4 Value iteration
Een nadeel van policy iteration is dat in elke iteratie een beleidsevaluatie-stap plaatsvindt die op
zich ook iteratieve berekeningen vergt. Bovendien vindt convergentie slechts plaats in de limiet;
dit wil zeggen, indien het beleid in twee opeenvolgende iteraties dezelfde is. De vraag kan gesteld
27

worden of het niet mogelijk is om reeds eerder het iteratieproces stop te zetten en toch het opti-
male bestelbeleid te vinden [21]. Een mogelijkheid is het in elke iteratie slechts eenmaal uitvoeren
van de beleidsevaluatie-stap (voor elke toestand s) in plaats van verder te gaan tot er convergentie
optreedt. Deze derde populaire oplossingsmethode, ontwikkeld door Bellman [1] wordt ’value
iteration’ genoemd. Dit is een methode gebaseerd op het principe van achterwaartse inductie.
In dit algoritme word de φ-reeks op zich niet gebruikt maar wordt gebruik gemaakt van de zo-
genaamde ’Bellman-vergelijking’ die bekomen wordt door het substitueren van de formule voor
φ(s) (formule (2.14)) in de formule voor V (s) (formule (2.15)):
Vk+1(s) = maxa
E[rt+1 + γ · Vk(st+1)|st = s, at = a
]= max
a
{∑s′
Pa(s, s′) ·[Ra(s, s
′) + γ · Vk(s′)]}
(2.16)
Met andere woorden, de waarde van een bepaalde toestand wordt gedefinieerd als de som van
de maximale verwachte kost in die toestand en de verwachte verdisconteerde waarde van alle
mogelijke toestanden s′ die vanuit toestand s kunnen bereikt worden.
Het value iteration algoritme bestaat vervolgens uit het iteratief oplossen van de Bellman-vergelijking
voor elke toestand s. Value iteration heeft in theorie echter een oneindig aantal iteraties nodig om
tot de optimale waarden voor V ∗ te komen. In praktijk is het algoritme dan ook voltooid indien
een epsilon-optimale oplossing wordt gevonden. Een nadeel van value iteration is dat er pas op
het einde van de iteraties een oplossing wordt gevonden, in tegenstelling tot policy iteration waar
de oplossing (het bestelbeleid) stelselmatig wordt verbeterd, hetgeen meer inzichtelijk is. Bij zeer
grote problemen kan via policy iteration bijgevolg ook een degelijke, maar nog niet optimale,
oplossing gevonden worden in een redelijke oplossingstijd. Bij value iteration is dit onmogelijk.
Een meer gedetailleerde weergave van dit algoritme kan eveneens gevonden worden in [8, Hoofd-
stuk 19] en [23].
2.2.5 Gauss-Seidel value iteration
De aangepaste versie van het value iteration algoritme die ook zal gebruikt worden in deze mas-
terproef is het ’Gauss-Seidel’s value iteration’ algoritme. Net als bij het oorspronkelijke algoritme
wordt de Bellman-vergelijking iteratief opgelost, maar in deze variant wordt Vk+1(s) gebruikt in
plaats van Vk(s). Omwille van deze aanpassing treedt convergentie sneller op bij grote toestands-
ruimtes.
28

2.3 Het toepassen van deze theorie doorheen de masterproef
Een van de eerste beslissingen die moet gemaakt worden is de keuze tussen de totale verdiscon-
teerde en de gemiddelde kost als kostencriterium. Volgens [8] is het aangewezen om de verdis-
conteerde kost te gebruiken indien de tijdsintervallen van de Markov-ketens voldoende lang zijn.
In deze situatie wordt immers de tijdswaarde van geld belangrijk. Of dit het geval is bij voor-
raadbeheer hangt uiteraard sterk af van de specifieke situatie. ’Fast-moving consumer goods’ of
’FMCG’s’5 worden vaak dagelijks aangevuld, terwijl duurzame luxeproducten soms slechts maan-
delijks worden aangevuld. In sectie 1.1.2 werd reeds het onderscheid gemaakt tussen periodieke
en continue modellen voor voorraadbeheer. Bij FMCG’s wordt de voorraad meestal elke dag en
bijgevolg periodiek gecontroleerd en wordt de voorraad opnieuw aangevuld tot het gewenste voor-
raadniveau. Een continue controle van het voorraadniveau daarentegen waarbij de voorraad wordt
aangevuld van zodra een gespecificeerde drempelwaarde wordt bereikt, wordt vaker gebruikt bij
producten met een lagere omloopsnelheid. Het model in deze masterproef, waarbij besteld wordt
afhankelijk van het voorraad- en prijsniveau vertoont meer gelijkenissen met dit tweede, continue
voorraadbeheer-systeem. De modellen die in de volgende hoofdstukken zullen besproken worden
zullen bijgevolg beter geschikt zijn voor deze tweede categorie van producten die een lagere om-
loopsnelheid kennen en daaruit volgend de tijdsintervallen groter zijn. Bovendien lijkt het ook
weinig realistisch voor de meeste producten dat de prijs sterk fluctueert op de zeer korte termijn
(dagelijks). Omwille van deze redenen zal het model beter toepasbaar zijn op producten waarbij
zowel vraag- als prijswijzigingen zich op de middellange termijn voordoen. Het logische gevolg
hiervan is dat er rekening zal moeten gehouden worden met de tijdswaarde van geld en de totale
verdisconteerde kost zal gebruikt worden als kostencriterium. Indien de prijs echter zodanig vola-
tiel is dat deze fluctueert op de zeer korte termijn kan het model echter zeer snel aangepast worden.
Enkel de gebruikte oplossingsmethode moet in dit geval aangepast worden aan het nieuwe kos-
tencriterium, namelijk de gemiddelde kost. Bovendien blijkt uit het oplossen van de modellen
uit de volgende hoofdstukken dat de resultaten met deze alternatieve oplossingsmethode niet of
nauwelijks wijzigen.
De keuze voor het gebruik van de verdisconteerde kost impliceert evenwel dat een geschikte
waarde moet gekozen worden voor de disconteringsfactor γ (zie formule (2.10)). De waarde
voor γ ligt over het algemeen dicht bij een, maar deze factor hangt vanzelfsprekend sterk af van
de grootte van het tijdsinterval. Een kost zal immers sterker moeten verdisconteerd worden indien
een tijdsinterval van een maand gebruikt wordt ten opzichte van een week. Niettemin mag men
niet te licht gaan over deze keuze aangezien deze een sterke invloed kan hebben op het resultaat.
Indien de kosten sterk verdisconteerd worden zal de onmiddellijke bestelkost immers veel sterker5FMCG: Laagwaardige consumentenproducten op winkelniveau met een hoge omloopsnelheid
29

doorwegen ten opzichte van de voorraadkost die ten laste valt van de toekomstige tijdsperiodes.
Hierdoor zal in grotere hoeveelheden besteld worden, waardoor de bestelkost kan worden toege-
wezen aan een groter aantal eenheden.
Een bijkomend voordeel van de keuze voor de verdisconteerde kost als kostencriterium is dat het
model eenvoudig kan aangepast worden tot een Markoviaans beslissingsproces met een eindige
tijdshorizon. Dit kan bijvoorbeeld van belang zijn bij producten die het gevolg zijn van een hype
en bijgevolg slechts een of enkele seizoenen verkocht worden.
Voor het ontwerpen van het beoogde voorraadmodel zal een discrete, stationaire Markov-keten op-
gesteld worden waarbij de toestandsruimte bestaat uit twee ’dimensies’ of ’toestandsvariabelen’.
Dit zijn enerzijds het prijsniveau en anderzijds het voorraadniveau. Deze Markov-keten zal gecon-
strueerd worden op basis van twee afzonderlijke Markov-ketens voor het voorraad- en prijsniveau.
De Markoviaanse eigenschap (zie sectie 2.1.1) impliceert in deze situatie dat noch de prijs uit het
verleden, noch het voorraadniveau uit het verleden een invloed heeft op de toekomstige evoluties.
Om de overzichtelijkheid en benodigde computertijd onder controle te houden zal gestart worden
met een kleine toestandsruimte. Hierdoor wordt een ’explosie’ van de toestandsruimte vermeden;
deze groeit namelijk exponentieel. Om dit te vermijden beperken we ons daarom in eerste instan-
tie tot twee prijsniveaus, ’laag’ en ’hoog’ (zie hoofdstuk 3). Het aantal mogelijke voorraadniveaus
zal in dit eerste vereenvoudigde model beperkt worden tot 4. Hierna zal getracht worden om deze
toestandsruimte uit te breiden en zodoende een meer algemeen toepasbaar model te bekomen (zie
hoofdstuk 4). In een laatste fase zal het model uitgebreid worden door het introduceren van een
variabele lead time om zodoende een meer algemeen toepasbaar model te bekomen (zie hoofd-
stuk 5). Hierbij zal met andere worden rekening gehouden worden met een tijdsverschil tussen het
bestellen van de goederen en het ontvangen ervan. Er worden twee belangrijke veronderstellingen
gemaakt inzake de Markov-keten, namelijk de beperking tot een eindig aantal mogelijke toestan-
den alsook de beperking tot stationaire overgangskansen en dus een stationaire Markov-keten (zie
sectie 2.1.1).
Vervolgens zal voor elke mogelijke actie (niets bestellen of x eenheden bestellen) een transitie-
en kostmatrix worden opgesteld die respectievelijk de kansen en de kosten weergeven die gepaard
gaan met de overgang van een toestand s naar een toestand s′. De overgangskansen tussen twee
toestanden in de transitiematrices worden bekomen door het vermenigvuldigen van de afzonder-
lijke overgangskansen betreffende de twee dimensies van de toestandsruimte. In formulevorm:
pi = Pr(∆voorraad)× Pr(∆prijs).
Het uiteindelijke doel is vervolgens het vinden van een optimaal beleid. Met andere woorden, het
30

vinden van de optimale lange-termijn beslissing bij elke mogelijke toestand uit de gedefinieerde
toestandsruimte. Met lange-termijn wordt geımpliceerd dat we niet op zoek zijn naar de actie of
beslissing die de kost minimaliseert in het eerstvolgende discrete tijdsinterval, maar wel de actie
die de totale verwachte verdisconteerde kost minimaliseert.
De vraagfluctuaties zullen zoals reeds eerder vermeld worden gemodelleerd door een geometri-
sche verdeling van de tijd tussen twee opeenvolgende inkomende bestellingen. Dit komt over-
een met de discrete versie van een exponentiele verdeling. Concreet houdt dit voor deze mas-
terproef in dat op elk discreet tijdstip de vraag naar goederen gelijk is aan een of afwezig is:
p = Pr(vraag) = Pr(voorraad − 1); dit is de kans op een voorraaddaling met een eenheid.
We hebben hier dus te maken met een discreet ./M/1 wachtlijnsysteem. In het geval van een
bestelling zal onmiddellijk geleverd moeten worden. Dit wil zeggen, als de voorraad uitgeput is
bij vraag gaat de vraag (en opbrengst) verloren. Er is met andere woorden geen ’backlog’6. De
kansverdeling voor het prijsniveau zal dan weer zodanig worden geconstrueerd dat dit prijsniveau
op korte termijn fluctueert rond een lange termijn gemiddelde prijs (zie hoofdstuk 4).
Verschillende scenario’s zullen worden uitgewerkt in verband met de prijsevolutie. Zo zal bijvoor-
beeld de invloed van zowel de frequentie als de amplitude van de fluctuaties bekeken worden, net
als de parameters die deze eigenschappen beınvloeden. Op deze manier kan geanalyseerd worden
hoe het bestelbeleid wijzigt indien het prijsniveau lange periodes een hoge, respectievelijk lage,
waarde aanneemt of indien dit prijsniveau snel fluctueert. Op basis van de resultaten van dit on-
derzoek zal dan getracht worden algemeen geldende, kwalitatieve conclusies te formuleren. Ook
de invloed van andere belangrijke parameters in het voorraadbeheer zal onderzocht worden. Deze
parameters zijn bijvoorbeeld de bestelkost, de voorraadkost, de vraag en de disconteringsfactor.
Bovendien zal ook gezocht worden naar de meest efficiente oplossingsmethode voor het model in
deze masterproef.
6De term ’backlog’ in het voorraadbeheer refereert naar een opeenstapeling van werk dat nog moet uitgevoerdworden of bestellingen die nog moeten behandeld worden
31

Hoofdstuk 3
Inleidend model met een beperktetoestandsruimte
In hoofstukken 1 en 2 werd de theorie aangehaald die noodzakelijk is om de wiskundige modellen
die in het licht van deze masterproef zijn ontwikkeld te kunnen begrijpen. Tevens werd toegelicht
hoe deze theorie zal toegepast worden en welke specifieke situaties zullen besproken worden. In
hoofdstukken 3, 4 en 5 worden nu de wiskundige modellen opgesteld en uitgebreid besproken.
3.1 Inleiding
In deze eerste fase van het onderzoek zal een vereenvoudigd model opgesteld en besproken wor-
den. In dit vereenvoudigd model wordt gewerkt met een zeer beperkte toestandsruimte en worden
ook een aantal belangrijke veronderstellingen gemaakt die niet altijd stroken met de bedrijfsre-
aliteit. In de volgende hoofdstukken zal deze toestandsruimte vervolgens sterk worden vergroot
en zullen ook enkele uitbreidingen bekeken worden, zoals het effect van een onzekere lead time.
Hierdoor wordt een meer realistisch en algemeen toepasbaar model bekomen. De beweegreden
om dit vereenvoudigde model in deze masterproef op te nemen is een grotere duidelijkheid bij
het uiteenzetten en weergeven van de verschillende componenten van het model. In de volgende
hoofdstukken zullen vervolgens louter de veranderingen en uitbreidingen besproken worden. Deze
aanpak moet het geheel overzichtelijker maken.
Zoals hierboven wordt vermeld, wordt de toestandsruimte in deze fase sterk beperkt door het aantal
mogelijke waarden in beide dimensies te beperken. In de eerste dimensie, het voorraadniveau, zijn
slechts vier waarden mogelijk, namelijk I = 1, 2, 3 of 4. Hierbij stelt ’I’ het voorraadniveau voor
en wordt de belangrijke veronderstelling gemaakt dat er steeds minstens 1 eenheid in voorraad
is en er altijd moet besteld worden in dit laagste voorraadniveau. In de tweede dimensie, het
32

prijsniveau, wordt het aantal waarden nog sterker beperkt en zal gewerkt worden met slechts 2
mogelijke prijsniveaus, ’hoog’ en ’laag’. Bovendien is de kans dat het systeem zich in een van
beide prijsniveaus bevindt even groot. Verder wordt ook het aantal mogelijke acties beperkt tot 3
mogelijkheden. Dit is enerzijds de actie ’niets bestellen’ en anderzijds de mogelijkheid om 2 of 3
eenheden te bestellen. Ook zal niet kunnen besteld worden vooraleer het voorraadniveau naar dit
laagste niveau is gezakt.
Een bijkomende veronderstelling die wordt gemaakt is dat bestellingen onmiddellijk geleverd wor-
den; er is met andere worden geen lead time en bijgevolg zal bij een bestelling op tijdstip t de
levering gebeuren op tijdstip t + 1. Als gevolg van deze veronderstelling wordt de onzekerheid
op het moment van bestellen sterk ingeperkt. Als een onzekere lead time geıncorporeerd wordt
in het model (zie hoofdstuk 5), ontstaat de mogelijkheid dat de voorraad volledig uitgeput raakt
vooraleer de bestelling geleverd wordt en gaat omzet verloren. In deze situatie wordt de kost van
verloren vraag zeer belangrijk. In dit vereenvoudigde model is deze kost echter nog irrelevant.
Als gevolg van deze veronderstellingen zullen de resultaten van dit model en de conclusies die
eraan gekoppeld kunnen worden, vrij algemeen van aard zijn en weinig toepassing kennen in de
bedrijfsrealiteit. Wel zal de invloed van bepaalde parameters kunnen onderzocht worden. Deze
parameters zijn bijvoorbeeld de frequentie waarmee de prijs fluctueert, de bestelkost en de voor-
raadkost. De mogelijkheid om aan een relatief goedkope prijs aan te kopen weegt mogelijk op
tegen een hogere voorraadkost.
3.2 Model
In deze sectie wordt het model stap voor stap besproken. Eerst zullen de marktfluctuaties gemo-
delleerd worden door twee Markov-ketens die gecombineerd worden tot een twee-dimensionale
Markov-keten met behulp van het Kronecker-product. Vervolgens zullen de mogelijke acties be-
sproken worden. Ten derde worden de transitiematrices weergegeven en besproken en ten slotte
ook de kostmatrices. In tabel 3.1 worden alle parameters weergegeven die in dit vereenvoudigde
model gebruikt worden.
Om de leesbaarheid te vergroten zal geregeld gebruik gemaakt worden van de notaties p, α en β,
zoals gedefinieerd in onderstaande tabel.
3.2.1 Markov-ketens
Zoals uitgebreid besproken in sectie 2.1.1 kan een Markov-keten beschreven worden als een proces
dat op probabilistische wijze evolueert in de tijd en hierbij door een aantal toestanden St beweegt.
33

Tabel 3.1: Gebruikte parameters in het vereenvoudigde model
Parameter Uitleg
p De kans op vraag op tijdstip tα De kans op een prijsdaling op tijdstip tβ De kans op een prijsstijging op tijdstip tC0 BestelkostCh VoorraadkostPL Laag prijsniveauPH Hoog prijsniveaud Disconteringsfactor
Parameter Definitie Uitleg
p 1− p De kans dat er geen vraag is op tijdstip tα 1− α De kans dat de prijs niet daaltβ 1− β De kans dat de prijs niet stijgt
De toestand van het systeem wordt vervolgens geobserveerd op discrete tijdstippen t. pij is de
kans dat het systeem beweegt naar toestand j vertrekkende van toestand i. Bovendien zegt de
Markoviaanse eigenschap dat de kansen inzake de toekomstige evolutie van het proces enkel af-
hankelijk zijn van de huidige toestand van het proces en dus onafhankelijk zijn van gebeurtenissen
of toestanden in het verleden. In deze masterproef worden 2 soorten marktfluctuaties in het model
opgenomen. Ten eerste is dit de fluctuatie van de prijs rond een lange-termijn gemiddelde. Ten
tweede zijn dit vraagfluctuaties op basis van een geometrische verdeling. Beide evoluties worden
gemodelleerd met behulp van een Markov-keten.
De vraagfluctuaties worden gemodelleerd op basis van een geometrische verdeling. Meer specifiek
houdt dit voor deze masterproef in dat op elk discreet tijdstip de vraag naar goederen een bedraagt
of afwezig is. De kans op vraag op een gegeven tijdstip wordt gegeven door ’p’. Dit is met
andere woorden de kans dat de voorraad daalt met een eenheid. Hieruit volgt logischerwijze dat
de kans dat de voorraad niet daalt binnen een tijdsinterval gelijk is aan 1 − p. De tijd tussen
twee opeenvolgende vragen is bijgevolg geometrisch verdeeld. Als gevolg van deze wijze van
modelleren hebben we hier te maken met een discreet ./M/1 wachtlijnsysteem. Het verminderen
van het voorraadniveau op basis van deze vraag wordt weergegeven in figuur 3.1. In deze figuur
daalt de voorraad op basis van de hierboven besproken kansverdeling. Indien het voorraadniveau
gezakt is naar een eenheid worden drie eenheden besteld. Hoe snel het voorraadniveau vermindert
hangt af van de grootte van p. In dit hoofdstuk is het ook mogelijk twee eenheden te bestellen in
plaats van drie, maar deze mogelijkheid is niet weergegeven in figuur 3.1.
34

t
V oorraadniveau
0 1 2 3 4 5 6 7 8 9 100
1
2
3
41
1
1
1
1
1
Figuur 3.1: Geometrische verdeelde vraag
Deze situatie kan gemodelleerd worden aan de hand van een Markov-keten en deze wordt grafisch
weergeven in figuur 3.2. Elke ’node’ (de cirkels op de figuur) stelt een mogelijke toestand voor
waarin het systeem zich kan bevinden. Elke pijl stelt een mogelijke overgang voor tussen twee
toestanden indien het systeem evolueert van tijdstip t naar tijdstip t + 1. p en 1 − p stellen de
respectievelijke overgangskansen voor die aan deze transities gekoppeld zijn. Indien bijvoorbeeld
vier eenheden in voorraad zijn en er komt een bestelling binnen (met kans p), dan zullen er op
tijdstip t+ 1 nog slechts drie eenheden in voorraad zijn. Indien er geen vraag is (met kans 1− p),
dan blijven er logischerwijze vier eenheden in voorraad. De keuze werd gemaakt om de voorraad
van hoog naar laag te ordenen teneinde het minderen van de voorraad bij vraag te visualiseren.
Indien geen actie ondernomen wordt zal het voorraadniveau als gevolg van deze Markov-keten
evolueren naar het laagste voorraadniveau, hetgeen overeenkomt met een eenheid. Er zijn immers
geen overgangspijlen in de omgekeerde richting. Indien niet besteld wordt is de kans dat het
systeem in dit laagste voorraadniveau blijft dus gelijk aan een.
4 3 2 1p p p
1− p 1− p 1− p 1
Figuur 3.2: Grafische voorstelling van de vraagfluctuaties door middel van een Markov-keten
De prijsfluctuaties worden eveneens gemodelleerd met behulp van een Markov-keten. In deze
eerste fase zijn slechts twee prijsniveaus mogelijk. Indien we α en β aan elkaar gelijkstellen is
de kans dat het systeem zich in een van beide prijsniveaus bevindt op een gegeven tijdstip gelijk
aan 50%. Deze situatie wordt grafisch weergegeven in figuur 3.3. De keuze werd gemaakt om
de prijs te ordenen van laag naar hoog. Deze keuze heeft als gevolg dat het uitzetten van de
35

bestelhoeveelheid in functie van het prijsniveau zal leiden tot een dalende functie.
PL PH
β
α
1− β 1− α
Figuur 3.3: Grafische voorstelling van de prijsfluctuaties door middel van een Markov-keten
De volledige toestandsruimte wordt vervolgens bekomen door beide dimensies (prijs en voorraad)
te combineren. Aangezien gewerkt wordt met 4 mogelijke voorraadniveaus en 2 mogelijke prijs-
niveaus zal het systeem zich in 8 mogelijke toestanden kunnen bevinden, zoals in tabel 3.2 wordt
weergegeven.
Tabel 3.2: Overzicht van de mogelijke toestanden Si waarin het systeem zich kan bevinden
Toestand Voorraadniveau Prijsniveau
S1 4 PLS2 4 PHS3 3 PLS4 3 PHS5 2 PLS6 2 PHS7 1 PLS8 1 PH
De combinatie van beide Markov-ketens vormt een nieuwe uitgebreide Markov-keten en wordt
grafisch weergegeven in figuur 3.4. De weergegeven overgangskansen worden bekomen door
het vermenigvuldigen van de overgangskansen uit de twee afzonderlijke Markov-ketens: pi =
Pr(∆voorraad)× Pr(∆prijs).
3.2.2 Eigenschappen van beide Markov-ketens
Deze gecombineerde Markov-keten, alsook de twee afzonderlijke Markov-ketens, kan omschre-
ven worden als een discrete, stationaire Markov-keten waarbij de toestandsruimte bestaat uit twee
dimensies. Het eerste deel van deze omschrijving betekent dat we hier te maken hebben met een
discrete-tijd Markov-keten, waarbij de toestand van het systeem slechts geobserveerd wordt op
discrete tijdstippen in tegenstelling tot het continu observeren. Het tweede deel geeft aan dat de
overgangskansen pij van deze Markov-keten stationair zijn en dus met andere woorden niet wijzi-
36

4, PH 3, PH 2, PH 1, PH
4, PL 3, PL 2, PL 1, PL
p · α p · α p · α
p · β p · β p · β
p · α p · β p · α p · β p · α p · β p · α p · β
p · α
p · β
p · α
p · β
p · α
p · β
p · α p · α p · α p · α
p · β p · β p · β p · β
Figuur 3.4: Grafische voorstelling van de marktfluctuaties door middel van een Markov-keten
gen in de tijd. Een derde eigenschap die moet vermeld worden is dat gewerkt zal worden met een
’oneindige horizon’, dit in tegenstelling tot een beperkt tijdsinterval.
Lange-termijn eigenschappen van de Markov-ketens
Een interessante eigenschap van Markov-ketens is het al dan niet bestaan van ’steady state kansen’
π (zie sectie 2.1.2). Deze kansen geven de waarschijnlijkheid weer dat het systeem zich in een
bepaalde toestand bevindt, onafhankelijk van de initiele toestand. Zoals reeds vermeld zijn deze
lange termijn kansen voor beide prijsniveaus gelijk aan 50% in de Markov-keten die de prijsfluctu-
aties voorstelt (i.e. in het geval dat α = β). In de Markov-keten die de vraagfluctuaties weergeeft
is de kans 100% dat na verloop van tijd het laagste voorraadniveau wordt bereikt.
Deze steady-state kansen kunnen eenvoudig worden berekend aan de hand van vergelijkingen (2.7)
en (2.8). In het geval van de Markov-keten die het prijsniveau modelleert worden deze vergelij-
kingen als volgt ingevuld:
πPL = πPL · pPLPL + πPH · pPHPLπPH = πPL · pPLPH + πPH · pPHPH1 = πPH + πPL
⇐⇒
πPL = πPL · (1− β) + πPH · α
πPH = πPL · β + πPH · (1− α)
1 = πPH + πPL
De steady-state vergelijkingen resulteren altijd in een stelsel met n onbekenden en n+ 1 vergelij-
kingen, waarbij n het aantal toestanden voorstelt. Er is bijgevolg steeds een overbodige vergelij-
king en het stelsel is steeds oplosbaar.
37

De oplossing:
πPL = 0.5
πPH = 0.5(3.1)
Deze te verwachten uitkomst is uiteraard enkel geldig in het geval dat de kans op een prijsstijging
gelijk is aan de kans op een prijsdaling. Indien de kans op een prijsdaling α groter zou zijn dan de
kans op een prijsstijging β zal de steady-state kans dat het systeem zich in het hogere prijsniveau
bevindt logischerwijze groter zijn. Indien bijvoorbeeld de kans op een prijsdaling twee maal zo
groot is als de kans op een prijsstijging wordt de volgende oplossing bekomen:
De oplossing:
πPL = 2/3
πPH = 1/3(3.2)
Voor het voorraadniveau worden deze vergelijkingen als volgt ingevuld. De resultaten zijn onaf-
hankelijk van de grootte van p. De kans dat op lange termijn het laagste voorraadniveau bereikt
wordt is dus gelijk aan 100%:
π4 = π4 · (1− p)
π3 = π4 · p+ π3 · (1− p)
π2 = π3 · p+ π2 · (1− p)
π1 = π2 · p+ π1 · 1
1 = π4 + π3 + π2 + π1
⇐⇒
π4 = 0
π3 = 0
π2 = 0
π1 = 1
De bovenstaande analyse heeft betrekking op de Markov-ketens zelf en situeert zich dus in het
geval er geen bestellingen worden geplaatst. Indien dit wel mogelijk is hebben we te maken met
een Markoviaans beslissingsproces, zoals in de volgende sectie wordt uitgelegd. Als in het verdere
verloop van deze masterproef de toestandsruimte uitgebreid wordt, zullen de steady state kansen
een grotere rol krijgen, bijvoorbeeld bij het analyseren van de frequentie van de prijsfluctuaties.
(zie sectie 4.2.1).
3.2.3 Markoviaans beslissingsproces
De bovenstaande redenering heeft enkel betrekking op Markov-ketens en stelt dus een passief
proces voor. We kunnen echter nog een stap verder gaan door proactief te werken en de werking
38

van het systeem aan te passen om op deze manier de prestaties te optimaliseren. Bij Markov-
beslissingsprocessen wordt bij elke mogelijke toestand Si van de Markov-keten een beslissing
di genomen over het ondernemen van een bepaalde actie, genomen uit een verzameling van K
mogelijke acties (k = 1, 2, . . . ,K). De actie die gekozen wordt heeft een invloed op zowel de
overgangskansen (zie sectie 3.2.4) als op de onmiddellijke en toekomstige kosten (zie sectie 3.2.5)
en op het gedrag van het systeem in de toekomst. Het is mogelijk dat bepaalde beslissingen
niet relevant zijn voor bepaalde toestanden. Het doel is vervolgens het vinden van de optimale
actie in elke toestand om zodoende deze kosten Cik te minimaliseren. Het beslissingsproces dat
hiermee gepaard gaat, wordt een Markoviaans beslissingsproces genoemd. In tabel 3.3 worden
deze begrippen overzichtelijk weergegeven.
Tabel 3.3: Gebruikte parameters in het vereenvoudigde model
Parameter Uitleg
St De toestand (voorraad, prijs) op tijdstip tdi De actie die ondernomen wordt in toestand ipij Pr{St+1 = j|St = i}Cik De kost indien actie k ondernomen wordt in toestand i
Pd(s, s′) Transitiematrix
Rd(s, s′) Kostmatrix
In dit hoofdstuk zijn er slechts twee mogelijke acties waaruit de beslissingsnemer kan kiezen, na-
melijk twee eenheden bestellen of drie eenheden bestellen. Deze twee acties stellen respectievelijk
de acties d2 en d3 voor. De eerste actie d1 heeft betrekking op het ’niet bestellen’ en hierbij wordt
bijgevolg passief de evolutie door de tijd van de Markov-keten gevolgd. De volgende notaties
zullen worden gebruikt:
Notatie Definitie Uitleg
d1 Actie 1 Niets bestellen
d2 Actie 2 2 eenheden bestellen
d3 Actie 3 3 eenheden bestellen
In dit vereenvoudigde model veronderstellen we bovendien dat er enkel kan besteld worden op het
laagste voorraadniveau, als er slechts een eenheid in voorraad is. Figuur 3.5 geeft deze situatie
grafisch weer. De groene en blauwe overgangspijlen stellen de mogelijke overgangen voor indien
respectievelijk actie d2 of d3 gekozen wordt. De toestand waarin het systeem terechtkomt in
tijdstip t + 1 hangt verder af van het al dan niet aanwezig zijn van vraag, weergegeven door de
39

kans p. De zwarte overgangspijlen stellen de situatie voor waarbij niets besteld wordt.
4 3 2 1
p
p
p
p
Actie 1 (d1): 0 eenheden bestellen
Actie 2 (d2): 2 eenheden bestellen
Actie 3 (d3): 3 eenheden bestellen
Figuur 3.5: Mogelijke acties en overgangen in het Markoviaans beslissingsproces
Indien ook de tweede dimensie, het prijsniveau, geıncorporeerd wordt, wordt een deel van het
Markoviaans beslissingsproces weergegeven in figuur 3.6. In deze figuur wordt verondersteld
dat het systeem zich in de toestand bevindt waarbij het voorraadniveau gelijk is aan een en het
prijsniveau gelijk is aan ’PL’. In deze toestand wordt vervolgens gekozen voor het bestellen van
twee eenheden (’actie 2’).
1, PL d2
2, PL 3, PL
2, PH 3, PH
p · (1− β)(1− p) · (1− β)
p · β (1− p) · β
Figuur 3.6: Mogelijke transities na het kiezen van actie d2
Dit model voldoet aan de Markoviaanse eigenschap aangezien we (1) te maken hebben met een
Markov-keten, (2) de nieuwe overgangskansen enkel afhankelijk zijn van de huidige toestand en
de beslissing, en (3) de onmiddellijke verwachte kost eveneens enkel afhankelijk is van de huidige
toestand en de beslissing. Deze kost bestaat namelijk uit twee elementen, de voorraadkost en de
eventuele aankoopkost. De voorraadkost is de kost die gepaard gaat met het houden van voorraad
en is bijgevolg enkel afhankelijk van het huidige voorraadniveau. De aankoopkost is dan weer
40

enkel afhankelijk van de gekozen actie (en bijgevolg bestelhoeveelheid) en de huidige prijs.
3.2.4 Transitiematrices
In een Markoviaans beslissingsproces zijn twee categorieen van matrices van belang. Ten eerste
zijn dit de transitiematrices P (s, s′, a). Deze geven de kans weer om toestand s′ te bereiken op
tijdstip t+ 1 als het systeem zich in toestand s bevindt op tijdstip t en actie a is ondernomen door
de beslissingsnemer. Een tweede categorie van matrices zijn de kostmatrices of beloningsmatrices;
R(s, s′, a) is de beloning die verworven wordt wanneer het systeem zich in toestand s bevindt op
tijdstip t en in toestand s′ op tijdstip t+ 1 na het kiezen van actie a
Gegeven de huidige toestand (voorraad- en prijsniveau) St op tijdstip t worden de kansen voor de
overgang naar de volgende toestand St+1 op tijdstip t+ 1 gegeven door een een-staps overgangs-
matrix of transitiematrix. Deze matrix geeft met andere woorden weer welke toestanden bereikt
kunnen worden vanuit een gegeven toestand en hoe groot de kans is om in elk van deze toestanden
te belanden. Elk element van deze matrix kan dus geschreven worden als pij = Pr{St+1 = j|St =
i}. Deze matrix, genoteerd als Pa(St, St+1) is afhankelijk van de gekozen actie di of a. Aangezien
we te maken hebben met een stationaire Markov-keten zijn de transitiematrices onafhankelijk van
de tijd:
∀i, j : Pr{St+1 = j|St = i} = Pr{S1 = j|S0 = i},∀t = 1, 2, . . . (2.2)
Transitiematrix zonder actie
De volledige transitiematrix bestaat uit twee dimensies, het voorraadniveau en het prijsniveau.
Beide dimensies kunnen afzonderlijk opgesteld en weergegeven worden, waarna ze via het ’Kro-
necker product’ omgezet worden in de volledige 8 × 8 transitiematrix. Hieronder wordt eerst het
effect van het Kronecker product (genoteerd als ⊗) weergegeven:
a b
c d
⊗e f
g h
=
ae af be bf
ag ah bg bh
ce cf de df
cg ch dg dh
(3.3)
De transitiematrix in het geval waarbij geen bestelling wordt geplaatst wordt hieronder weerge-
geven. Omwille van de beperkte toestandsruimte zou het mogelijk zijn om de volledige twee-
dimensionale Markov-keten in zijn geheel weer te geven. Echter, met het oog op de uitbreiding
van de toestandsruimte wordt er gekozen om deze als Kronecker product van de twee afzonderlijke
Markov-ketens weer te geven. In essentie zijn deze matrices enkel een alternatieve weergave van
41

figuren 3.2 en 3.3. De volledige transitiematrix is dan een alternatieve weergave van figuur 3.4.
Merk op dat de elementen in deze transitiematrices de kansen voorstellen van een transitie van de
’rij-toestand’ naar de ’kolom-toestand’.
V oorraad 4 3 2 1
4 1− p p 0 0
3 0 1− p p 0
2 0 0 1− p p
1 0 0 0 1
⊗
Prijs PL PH
PL 1− β β
PH α 1− α
Ter illustratie worden de eerste twee en de laatste twee rijen van de volledige transitiematrix hier-
onder weergegeven. De definitie van de toestanden S1, S2, . . . , S8 werd reeds gegeven in tabel 3.2.
St | St+1 S1 S2 S3 S4 S5 S6 S7 S8
S1 (1− p) · (1− β) (1− p) · β p · (1− β) p · β 0 0 0 0
S2 (1− p) · α (1− p) · (1− α) p · α p · (1− α) 0 0 0 0
De laatste twee rijen:
St | St+1 S1 S2 S3 S4 S5 S6 S7 S8
S7 0 0 0 0 0 0 β
S8 0 0 0 0 0 0 α
Deze laatste twee rijen van de transitiematrix zijn echter irrelevant aangezien in deze situatie het
laagste voorraadniveau is bereikt en er verondersteld wordt dat er dan zeker besteld wordt. Dit zal
afgedwongen worden in de kostmatrix door een zeer hoge kost toe te kennen aan de actie ’niets
bestellen’ in toestanden S7 en S8.
Deze matrix heeft enkele belangrijke en karakteristieke eigenschappen. In elke rijvector zijn alle
waarden namelijk positief en is hun som gelijk aan een. Dergelijke vectoren worden ’kansvecto-
ren’ genoemd. Een matrix waarbij alle rijvectoren kansvectoren zijn, wordt een transitiematrix of
stochastische matrix genoemd.
In essentie geven deze matrices schematisch weer dat op elk tijdstip t het systeem zich in een
bepaalde toestand St bevindt. Vervolgens evolueert het systeem op probabilistische wijze naar
een nieuwe toestand St+1, op basis van de kansen α, β en p. De transitiematrix geeft weer welke
overgangen mogelijk zijn vanuit een bepaalde toestand en hoe groot de kans is om in een bepaalde
toestand terecht te komen. In elke rij is de som van alle kansen dan ook bij definitie gelijk aan een.
42

Transitiematrices met actie
Het nemen van een actie (het bestellen van 2 of 3 eenheden) zorgt ervoor dat deze matrix er anders
gaat uitzien. De beslissing of actie di = k beınvloedt de overgangskansen pij(k) voor de overgang
van de huidige toestand Si naar de volgende toestand. Aangezien in dit vereenvoudigd model
verondersteld wordt dat er enkel in het laagste voorraadniveau kan besteld worden, veranderen
enkel de laatste twee rijen van bovenstaande matrix. Bij een bestelling van twee eenheden gebeurt
dit als volgt:
St | St+1 S1 S2 S3 S4 S5 S6 S7 S8
S7 0 0 (1− p) · (1− β) (1− p) · β p · (1− β) p · β 0 0
S8 0 0 (1− p) · α (1− p) · (1− α) p · α p · (1− α) 0 0
Bij een bestelling van drie eenheden:
St | St+1 S1 S2 S3 S4 S5 S6 S7 S8
S7 (1− p) · (1− β) (1− p) · β p · (1− β) p · β 0 0 0 0
S8 (1− p) · α (1− p) · (1− α) p · α p · (1− α) 0 0 0 0
De grootte van de overgangskansen op zich wijzigt met andere woorden niet als gevolg van het
plaatsen van een bestelling. Deze kansen schuiven enkel twee, respectievelijk drie voorraadniveaus
op naar links, naar een hoger voorraadniveau. De overige rijen zijn irrelevant aangezien deze acties
hier niet mogelijk zijn.
Elke beslissing die genomen wordt, in een bepaalde toestand of op een bepaald tijdstip, beınvloedt
niet enkel de toestand van het systeem op tijdstip t + 1, maar ook de evolutie van het systeem in
de toekomst. Aangezien aan elke toestand en aan elke beslissing een bepaalde kost is verbonden,
beınvloedt elke actie bijgevolg zowel de onmiddellijke en toekomstige kosten. Welke actie uitein-
delijk gekozen wordt zal afhangen van de lange termijn kosten die aan deze actie verbonden zijn.
Uiteindelijk zal in elke mogelijke toestand die actie gekozen worden die de lange termijn verdis-
conteerde kosten minimaliseert. Zo zal bijvoorbeeld in de beslissing om twee of drie eenheden
te bestellen een afweging moeten worden gemaakt tussen een hogere voorraadkost en een hogere
bestelkost per eenheid.
Het vastleggen van een optimale beslissing di in elke mogelijke toestand resulteert in een beleid
of ’policy’. Zoals reeds vermeld in sectie 2.1.3 wordt dit bestelbeleid gekenmerkt door twee
belangrijke eigenschappen:
1. Een beleid is stationair. Als een systeem zich in een bepaalde toestand Si bevindt, zal de
beslissing steeds dezelfde zijn, onafhankelijk van het tijdstip t.
43

2. Een beleid is deterministisch. Als een systeem zich in toestand i bevindt, zal er steeds een
welbepaalde beslissing genomen worden. Dit in tegenstelling tot een ’randomized policy’
waar een kansverdeling gebruikt wordt voor het selecteren van een beslissing.
3.2.5 Kostmatrices
Indien een beslissing di = k genomen wordt in toestand Si dan gaat hiermee een kostCik gepaard.
De kosten verbonden aan het houden van voorraad kunnen worden opgesplitst in ’aankoopkosten’
en ’voorraadkosten’. Beide kosten zullen afzonderlijk besproken worden.
In overeenstemming met de transitiematrices kan ook deze informatie met behulp van matrices
gemodelleerd worden. Deze matrix wordt genoteerd als Ra(St, St+1) of Rd(St) indien de kost op
tijdstip t onafhankelijk is van de toestand waarin het systeem terechtkomt op tijdstip t+ 1. Zowel
de voorraadkost als de aankoopkost zijn inderdaad enkel afhankelijk van de huidige toestand en
de beslissing die genomen wordt in verband met het al dan niet bestellen. Als later in hoofdstuk
5 het model uitgebreid wordt door het introduceren van een stochastische lead time, zal ook de
kost van verloren vraag in het model opgenomen worden. Dit is de kost die gepaard gaat met de
situatie waarbij er vraag is maar hier niet aan voldaan kan worden omdat de voorraad uitgeput is.
Voorraadkost
Een eerste kost die onlosmakelijk verbonden is met voorraadbeheer is de ’holding cost’. Deze
is opgebouwd uit enerzijds de opportuniteitskosten van het vastgelegde kapitaal en anderzijds de
kosten voor de opslag en het interne transport van de goederen. In het vervolg van deze mas-
terproef wordt verondersteld dat het geheel van deze drie kosten omvat wordt door het begrip
’voorraadkosten’. Afhankelijk van het type product kan deze kost hoog oplopen, bijvoorbeeld in
het geval dat de goederen continu moeten gekoeld worden. Deze kost is onafhankelijk van zo-
wel het prijsniveau als de beslissing die genomen wordt en dus enkel afhankelijk van het huidige
voorraadniveau. Indien de voorraadkost per eenheid voorraad genoteerd wordt als ’Ch’ worden
kosten verkregen zoals weergegeven in onderstaande beknopt weergegeven matrix. Hierbij wordt
verondersteld dat deze voorraadkost recht evenredig is met het voorraadniveau.
V oorraad St+1
4 4 · Ch3 3 · Ch2 2 · Ch1 1 · Ch
44

Aankoopkost
De aankoopkosten zijn vanzelfsprekend enkel relevant in het geval een bestelling geplaatst wordt,
dus indien actie d2 of d3 gekozen wordt. Deze kosten omvatten enerzijds de vaste bestelkosten C0
en anderzijds de variabele aankoopkosten per eenheid of met andere worden de prijs.
In tegenstelling tot de voorraadkosten zijn de aankoopkosten wel afhankelijk van het prijsniveau
en van de beslissing die genomen wordt, maar niet van het huidige voorraadniveau. Met actie d1gaat geen aankoopkost gepaard en de bijhorende kostmatrix is bijgevolg gelijk aan de nulmatrix.
Bij acties d2 en d3 is deze kost uiteraard wel aanwezig. Deze is gelijk aan C0 + x · Pt waarbij
x gelijk is aan de bestelhoeveelheid en Pt de prijs op het ogenblik van bestellen voorstelt. De
verschillende mogelijkheden worden hieronder in matrixvorm weergegeven:
Prijs | Actie d1 d2 d3
PL 0 C0 + 2 · PL C0 + 3 · PLPH 0 C0 + 2 · PH C0 + 3 · PH
Totale kost
De kostmatrices Ra(St, St+1) worden eenvoudig bekomen door het optellen van de voorraadkost
en de aankoopkost zoals hierboven weergeven. Er zijn bijgevolg drie verschillende kostmatrices,
een voor elke mogelijk actie, die overeenkomen met de drie transitiematrices die zijn opgesteld in
sectie 3.2.4.
Deze matrices, met ingevulde waarden voor de verschillende parameters, zijn voldoende input
om het Markoviaans beslissingsproces op te lossen. Het optimale bestelbeleid kan nu berekend
worden met behulp van een van de oplossingsmethodes die besproken zijn in sectie 2.2. Hier-
bij wordt rekening gehouden met een aantal trade-offs zoals besproken in sectie 1.1. De lagere
gemiddelde prijs die betaald wordt per eenheid bij een grote bestelling moet immers afgewogen
worden tegenover de voorraadkost.
3.3 Resultaten
Voor het opstellen en oplossen van bovenstaand model werd gebruik gemaakt van de technische
software omgeving van Matlab. Dit programma, ontwikkeld door Mathworks, wordt gebruikt voor
allerhande wiskundige toepassingen en is uiterst geschikt voor het efficient werken met matrices.
Voor het oplossen van de Markoviaanse beslissingsprocessen werd gebruik gemaakt van de ’MDP
Toolbox’ waarbij MDP staat voor ’Markov Decision Processes’ ofwel Markoviaanse beslissings-
processen. Deze toolbox kan gezien worden als een uitbreiding van de functies die inherent in
45

Matlab aanwezig zijn en bevat onder andere software code voor de verschillende oplossingsme-
thodes zoals besproken in sectie 2.2.
De resultaten van dit vereenvoudigd model zijn de resultaten die ook na logisch nadenken verwacht
kunnen worden. De korte uiteenzetting van deze resultaten heeft dan ook gedeeltelijk als doel het
inzicht in de verschillende factoren van het voorraadbeheer aan te scherpen. In deze sectie zal de
invloed van een aantal parameters op het bestelbeleid worden onderzocht. Deze parameters zijn de
prijs, de voorraadkost, de bestelkost en de prijsevolutie. Verder zal ook onderzocht worden welke
oplossingsmethode dit probleem op de meest efficiente wijze oplost.
Het bestelbeleid is steeds een afweging of trade-off tussen de verschillende kosten die gepaard
gaan met voorraadbeheer, meer specifiek de voorraadkost en de aankoopkost. Zo zal een afweging
moeten gemaakt worden tussen een hogere voorraadkost en een hogere bestelkost per eenheid. Bij
een hoge bestelkost en een hoog prijsniveau bijvoorbeeld kan de kans op een prijsdaling er voor
zorgen dat het systeem een klein aantal goederen bestelt ondanks de hoge bestelkost.
3.3.1 Invloed van de prijs op het bestelbeleid
Uit dit vereenvoudigde model kunnen logischerwijze geen grote conclusies getrokken worden.
Zolang de bestelkost of de voorraadkost niet een bepaalde drempel of ’threshold’ overschrijdt zal
de voorraad
1. volledig worden aangevuld wanneer het prijsniveau laag is (actie d2).
2. gedeeltelijk worden aangevuld wanneer het prijsniveau hoog is (actie d3).
Deze situatie wordt weergegeven in onderstaande tabel en in figuur 3.7 waarbij zoals veronder-
steld enkel in het laagste voorraadniveau besteld wordt. De toestanden komen overeen met deze
gedefinieerd in tabel 3.2.
Tabel 3.4: Invloed van de prijs op het bestelbeleid
Voorraad Prijs Policy Bestelhoeveelheid
4 PL d1 04 PH d1 03 PL d1 03 PH d1 02 PL d1 02 PH d1 01 PL d3 31 PH d2 2
46

0
1
2
3
4
Laag Hoog Laag Hoog Laag Hoog Laag Hoog
4 4 3 3 2 2 1 1
Be
ste
lho
eve
elh
eid
Toestand (Prijs--Voorraad)
Figuur 3.7: Invloed van de prijs op het bestelbeleid
3.3.2 Invloed van de voorraadkost op het bestelbeleid
De relatieve grootte van de verschillende kosten die gepaard gaan met het bestellen van goede-
ren en het houden van voorraad heeft vanzelfsprekend een invloed op het bestelbeleid. Er zal
namelijk een afweging moeten gemaakt worden tussen een hogere voorraadkost en een hogere
bestelkost per eenheid. Indien de voorraadkost Ch per eenheid een bepaalde drempel overschrijdt
zal het namelijk niet langer voordelig zijn om het maximale aantal eenheden te bestellen. Het
bestellen van een groter aantal eenheden zorgt er dan ook voor dat de gemiddelde hoeveelheid
goederen in voorraad toeneemt en bijgevolg ook de gemiddelde voorraadkost per tijdseenheid. De
totale voorraadkost wordt immers weergegeven door formule (3.4) (zie hoofdstuk 1), waarbij Q
de bestelhoeveelheid voorstelt.
Ch ·Q
2(3.4)
Er zal dus bij een laag prijsniveau een afweging moeten gemaakt worden tussen enerzijds het
voordeel van het bestellen van meerdere eenheden aan een lagere prijs, en anderzijds de hogere
kost ten gevolge van het aanhouden van een grotere voorraad. Deze situatie is weergegeven in
figuur 3.8.
3.3.3 Invloed van de bestelkost op het bestelbeleid
In vergelijking met de voorraadkost heeft de bestelkost een vergelijkbare maar tegengestelde in-
vloed op het bestelbeleid. Van zodra een bepaalde drempel overschreden wordt, zal deze bestel-
kost per eenheid in de totale kost zwaarder doorwegen dan de voorraadkost. Deze totale bestelkost
wordt weergegeven in formule (3.5).
C0 ·D
Q(3.5)
47

0
1
2
3
4
Voorraadkost
Best
elh
oeve
elh
eid
Beleid in S
7 (P
L)
0
1
2
3
4
Voorraadkost
Best
elh
oeve
elh
eid
Beleid in S
8 (P
H)
Figuur 3.8: Invloed van de voorraadkost op het bestelbeleid
Dit heeft als gevolg dat een groter aantal eenheden per bestelling zal gekozen worden bij het mi-
nimaliseren van de totale verdisconteerde kost. Waar deze drempel zich zal bevinden is mede
afhankelijk van de disconteringsfactor d. Deze factor zorgt er namelijk voor dat de voorraadkost,
die zich deels in de nabije toekomst bevindt, minder belangrijk wordt ten opzichte van de bestel-
kost die volledig ten laste valt van het tijdstip waarop besteld wordt. De invloed van de bestelkost
op de bestelhoeveelheid wordt weergegeven in figuur 3.9.
0
1
2
3
4
Bestelkost
Be
ste
lho
eve
elh
eid
Policy in S
7 (P
L)
0
1
2
3
4
Bestelkost
Be
ste
lho
eve
elh
eid
Policy in S
8 (P
H)
Figuur 3.9: Invloed van de bestelkost op het bestelbeleid
3.3.4 Invloed van de prijsevolutie op het bestelbeleid
Het bestelbeleid zal ook afhangen van de relatieve kans op een prijsdaling ten opzichte van de
kans op een prijsstijging. Tot hiertoe werd steeds verondersteld dat deze twee kansen aan elkaar
gelijk zijn, resulterend in de 50% steady-state kansen in vergelijking (3.1) op pagina 38. Indien
echter de kans op een prijsdaling groter wordt dan de kans op een prijsstijging, dan veranderen
deze steady-state kansen. In vergelijking (3.2) wordt bijvoorbeeld de situatie weergegeven waarbij
de kans op een prijsdaling twee maal zo groot is als de kans op een prijsstijging.
48

In een dergelijke situatie wijzigt de trade-off tussen de verschillende kosten. In de specifieke si-
tuatie bijvoorbeeld waarbij omwille van een hoge bestelkost steeds het maximale aantal eenheden
besteld wordt, kan de grotere kans op een prijsdaling als gevolg hebben dat er toch een kleiner
aantal eenheden besteld wordt.
3.3.5 Vergelijking van de verschillende oplossingsmethodes
Tabel 3.5 geeft een overzicht van de efficientie van de verschillende oplossingsmethodes in het
oplossen van dit model. Deze oplossingsmethodes werden reeds besproken in sectie 2.2. De re-
sultaten bij elke oplossingsmethode zijn het gevolg van het duizend maal oplossen van het model,
waarna hiervan het gemiddelde genomen werd. De processor die werd gebruikt is een Intel(R)
Core i5 @2.80GHz, gecombineerd met 6GB geınstalleerd RAM-geheugen en een 64 bits bestu-
ringssysteem. Verder werd ook gebruik gemaakt van een 64-bits versie van Matlab 7.12.0.
Oplossingsmethode Aantal iteraties CPU-tijd [ms]
Lineair programmeren n.v.t. 7, 9
Policy iteration 2 2, 0
Policy iteration modified 3 2, 6
Value iteration 12 1, 4
Value iteration Gauss-Seidel 55 11, 0
Tabel 3.5: Vergelijking van de verschillende oplossingsmethodes
Onmiddellijk is duidelijk dat value iteration en policy iteration de meest efficientie methodes zijn
voor het oplossen van een dergelijk Markoviaans beslissingsproces. Hierbij valt op dat value
iteration een groter aantal iteraties nodig heeft om tot het optimale bestelbeleid te komen, maar
deze optimale oplossing wordt wel bereikt in een kortere tijd. Het is echter voorbarig al conclusies
te trekken op basis van deze kleine toestandsruimte. Veel interessanter zal zijn om te zien hoe
deze prestaties evolueren met een exploderende toestandsruimte. Op basis van deze resultaten
kan evenwel verwacht worden dat policy iteration de meest efficiente methode zal zijn bij het
oplossen van een model met een grotere toestandsruimte. Elke iteratie zal in dat geval immers meer
rekenwerk vergen en bijgevolg zou het aantal iteraties de doorslag kunnen geven. Dit vermoeden
wordt bevestigd in hoofdstuk 4.
49

Hoofdstuk 4
Model met een uitgebreidetoestandsruimte
4.1 Inleiding
In hoofdstuk 3 werden de relevante theoretische begrippen uitgelegd en geıllustreerd aan de hand
van een vereenvoudigd model. In dit hoofdstuk zal deze kennis gebruikt worden om een meer
algemeen toepasbaar model op te stellen en op te lossen. De toestandsruimte wordt sterk uitgebreid
en er zal onder andere bekeken worden tot hoever het aantal toestanden kan verhoogd worden
zodanig dat het optimale bestelbeleid nog steeds binnen ’redelijke’ tijd kan gevonden worden.
Hierbij zullen ook de prestaties van de verschillende oplossingsmethodes worden geevalueerd. In
deze fase van het onderzoek wordt evenwel nog geen levertermijn in het model opgenomen. Dit
zal wel het geval zijn in hoofdstuk 5.
Voorlopig wordt nog steeds verondersteld dat er verplicht besteld moet worden als het laagste
voorraadniveau is bereikt. Dit wordt opnieuw afgedwongen in de kostmatrix van het Markov-
beslissingsproces. Een andere mogelijkheid is het introduceren van een ’kost van verloren vraag’.
Deze kost is echter irrelevant in deze fase aangezien een lead time gelijk aan nul wordt veronder-
steld. Hierdoor zal steeds aan de vraag kunnen voldaan worden, zelfs indien gewacht wordt om te
bestellen tot de voorraad volledig is uitgeput. Deze kost van verloren vraag zou bijgevolg enkel
relevant zijn indien de prijs om de goederen aan te kopen hoger ligt dan de verkoopprijs van deze
goederen, maar met deze uitzonderlijke situatie wordt geen rekening gehouden. Bijgevolg wordt
verondersteld dat deze kost irrelevant is zolang gewerkt wordt zonder een onzekere levertermijn.
Als daarentegen in hoofdstuk 5 een levertermijn in het model wordt geıncorporeerd, zal deze kost
van verloren vraag wel een belangrijke invloed hebben op het bestelbeleid.
In figuur 4.1 wordt een voorbeeld gegeven van hoe het voorraadverloop er zou kunnen uitzien bij
50

het model dat besproken wordt in dit hoofdstuk; hierbij wordt de veronderstelling gemaakt dat het
maximale voorraadniveau gelijk is aan zes. In dit model wordt evenwel de mogelijkheid opgeno-
men dat de voorraad is uitgeput. Er is met andere woorden een voorraadniveau gelijk aan nul. Net
zoals in figuur 3.1 wordt nog steeds gewerkt met een vraag waarbij het tijdsinterval tussen twee
opeenvolgende bestellingen geometrisch verdeeld is. Op de figuur wordt de mogelijkheid weer-
gegeven om een willekeurige hoeveelheid goederen te bestellen vooraleer de voorraad uitgeput is.
Tevens is echter ook duidelijk dat het voorraadniveau niet op nul kan blijven aangezien dan zeker
een bestelling geplaatst wordt, tenzij slechts een eenheid besteld wordt en er een vraag is naar een
eenheid. Indien alle kosten en kansverdelingen constant blijven zoals in deze masterproef, zal het
tijdstip van bestellen en de bestelde hoeveelheid op een bepaald tijdstip enkel afhankelijk zijn van
het voorraad- en prijsniveau op dit tijdstip. Dit komt overeen met de Markoviaanse eigenschap.
Ook is in figuur 4.1 duidelijk weergegeven dat er gewerkt wordt met discrete tijdsintervallen.
t
V oorraadniveau
1
0
Figuur 4.1: Voorbeeld van een mogelijk voorraadverloop in het uitgebreide model
In overeenstemming met hoofdstuk 3 zal in sectie 4.2 de modellering van de betreffende pro-
bleemstelling uitgebreid worden uiteengezet. Hierbij zullen hoofdzakelijk de aanpassingen en
uitbreidingen ten opzichte van hoofdstuk 3 worden uitgelegd. Vervolgens zullen in sectie 4.3 de
belangrijkste resultaten worden voorgesteld.
4.2 Model
In deze sectie worden beknopt de aanpassingen besproken ten opzichte van het model uit hoofd-
stuk 3. Hierbij wordt verondersteld dat de lezer, op basis van de uiteenzetting in hoofdstuk 3,
reeds voldoende voorkennis heeft om de theoretische onderbouw van dit model te begrijpen. De
relevante parameters, weergegeven in tabel 3.1, worden verder uitgebreid met een aantal nieuwe
parameters. Deze worden voorgesteld in tabel 4.1.
51

Tabel 4.1: Overzicht en definitie van de nieuwe parameters en variabelen in hoofdstuk 4
Parameter Definitie Uitleg
Pi Prijsniveau iP (P1, P2, . . . , PK) Verzameling van mogelijke prijsniveausK Aantal mogelijke prijsniveausC Maximale voorraadniveau
In overeenstemming met hoofstuk 3 zullen eerst beide Markov-ketens opgesteld worden (sec-
tie 4.2.1). Vervolgens wordt de mogelijkheid tot het bestellen van goederen toegevoegd, resulte-
rend in een Markoviaans beslissingsproces (sectie 4.2.4). Het aantal mogelijke acties zal hierbij
een heel stuk hoger liggen in vergelijking met hoofdstuk 3 en gelijk zijn aan het maximale voor-
raadniveau. Bij elk voorraad- en prijsniveau zal namelijk moeten beslist worden of en hoeveel
eenheden er besteld zullen worden. Op basis van dit Markoviaans beslissingsproces worden ver-
volgens de transitie- en kostmatrices opgesteld voor elke mogelijke actie.
4.2.1 Markov-keten voorraadniveau
De vraagfluctuaties op basis van een geometrische verdeling worden gemodelleerd met behulp
van een Markov-keten die in essentie een eenvoudige uitbreiding is van de Markov-keten die be-
sproken werd in hoofdstuk 3. Enkel de toestandsruimte wordt sterk uitgebreid en tevens wordt het
voorraadniveau gelijk aan nul opgenomen in het model. Indien C het maximale voorraadniveau
voorstelt, kan het systeem zich bijgevolg inC+1 mogelijke toestanden bevinden. Figuur 4.2 geeft
deze Markov-keten grafisch weer. Net als in hoofdstuk 3 zal de steady state kans dat het systeem
zich op lange termijn in het laagste voorraadniveau bevindt, gelijk zijn aan een; dit is, indien geen
bestellingen worden geplaatst.
C C − 1 . . . 2 1 0p p p p p
1− p 1− p 1− p 1− p 1
Figuur 4.2: Grafische voorstelling van de vraagfluctuaties door middel van een Markov-keten
4.2.2 Markov-keten prijsniveau
De Markov-keten die de prijsfluctuaties modelleert is in tegenstelling tot de vraagfluctuaties wel
sterk aangepast ten opzichte van de Markov-keten in hoofdstuk 3. Er is vanaf heden niet enkel
een laag en een hoog prijsniveau, maar er wordt gewerkt met een verzameling van K mogelijke
52

prijsniveaus P = (P1, P2, . . . , PK). Deze Markov-keten wordt weergegeven in figuur 4.3.
Zoals weergegeven in figuur 4.3 werd er voor gekozen om de kans op een prijsstijging β (res-
pectievelijk prijsdaling α) met een welbepaalde factor v (hier 0.9 ofwel 10%) te laten afnemen
naarmate het prijsniveau verder verwijderd is van het gemiddelde prijsniveau. Indien het prijs-
niveau op een bepaald moment afwijkt van de gemiddelde prijs P zal hierdoor de kans dat het
systeem zich terug in de richting van deze gemiddelde prijs beweegt groter zijn dan de kans dat
het prijsniveau nog verder afwijkt van deze gemiddelde prijs. Verder is de kans dat het prijsniveau
onveranderd blijft op het volgende tijdstip steeds gelijk aan 1− (α+ β) en dus onafhankelijk van
het prijsniveau. Hierdoor zal de kans dat het prijsniveau wijzigt in de richting van het gemiddelde
prijsniveau steeds stijgen, aangezien de kans dat de prijs zich verder van het gemiddelde gaat
verwijderen kleiner worden. De totale som van deze drie kansen is uiteraard gelijk aan een.
P
P − 1
P + 1
P − 2
P + 2
P − 3
P + 3
. . .
. . .
P1
PK
α
β
γ10.9 · α
γ2
0.92 · α
γ3
0.93 · α
γ4
0.9I · α
γI
λ1
0.9 · β
λ2
0.92 · β
λ3
0.93 · β
λ4
0.9J · β
λJ
ω
ω ω ω 1− γI
ω ω ω 1− λJ
- Definities: ω = 1− (α+ β) ; γi = β + (α− 0.9i · α) ; λj = α+ (β − 0.9j · β)
- i = 1, . . . , I ; j = 1, . . . , J
Figuur 4.3: Grafische voorstelling van de prijsfluctuaties door middel van een Markov-keten
De redenering achter deze constructie is het creeren van prijsfluctuaties rond een lange-termijn
gemiddelde prijs waarbij de kans op deze gemiddelde prijs P het hoogst is. Indien deze kansen
onafhankelijk zouden zijn van de toestand waarin het systeem zich bevindt, zouden immers de
steady-state kansen voor alle prijsniveaus aan elkaar gelijk zijn, hetgeen ons weinig realistisch
lijkt. Deze situatie zou bijvoorbeeld ook als effect hebben dat enkel goederen besteld worden
indien de voorraad reeds uitgeput is en dus geen gebruik wordt gemaakt van een lagere prijs om
reeds vroeger goederen aan te kopen. De kans dat de prijs nog verder zakt is in deze situatie
immers even groot als de kans dat de prijs terug in de richting van de gemiddelde prijs evolueert.
53

Frequentie van de fluctuaties
De prijsfluctuaties zoals hierboven beschreven worden gekarakteriseerd door twee verschillende
grootheden, namelijk de frequentie en de amplitude. De frequentie van deze fluctuaties wordt
logischerwijze bepaald door de grootte van α en β. Indien deze kansen groter worden, zal de kans
om in hetzelfde prijsniveau (1 − (α + β)) te blijven kleiner worden en zal de volatiliteit van de
prijs bijgevolg een stuk hoger liggen. Dit kan er toe leiden dat het voordeliger wordt om van een
lage prijs gebruik te maken ook al zijn er nog voldoende goederen in voorraad. De kans op een
prijsstijging is immers groot.
Indien α en β van elkaar zouden verschillen verandert initieel enkel het gemiddelde prijsniveau;
de kenmerken van de kansverdeling blijven dezelfde. Indien deze kansen sterk van elkaar ver-
schillen vertoont de kansverdeling een exponentieel verloop. Op figuur 4.4 is ter illustratie de
kansverdeling van het prijsniveau weergegeven voor enkele waarden van α en β, in het geval er
41 mogelijke prijsniveaus bestaan (i.e. K = 41).
0
0,02
0,04
0,06
0,08
0,1
0,12
0,14
0,16
0,18
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41
Stea
dy-
stat
e ka
nse
n
Prijsniveau
a = b = 0,2
a = 0,25 ; b = 0,2
a = 0,3 ; b = 0,2
a = 0,35 ; b = 0,2
Figuur 4.4: Mogelijke kansverdelingen voor het prijsniveau in functie van α en β
Belangrijk om te vermelden is dat de absolute grootte van α en β geen invloed hebben op de
kansverdeling, maar enkel op de volatiliteit. Wat betreft de kansverdeling is enkel hun relatieve
grootte van belang.
Amplitude van de fluctuaties
De amplitude op haar beurt wordt bepaald door de snelheid waarmee de kans op een prijsdaling of
prijsstijging afneemt naarmate de prijs zich verder van het gemiddelde bevindt. In figuur 4.3 wordt
deze snelheid vastgelegd door de factor v = 0.9, maar het is uiteraard mogelijk de grootte van deze
factor aan te passen. Indien de grootte van deze overgangskansen slechts traag afneemt omwille
van een hoge waarde voor v, dan zal de kansverdeling van de prijsniveaus leptokurtisch van vorm
54

zijn. Dit betekent dat er een grote kans is dat het prijsniveau zich in de buurt van het lange-termijn
gemiddelde bevindt, maar een kleine kans dat een extreem (hoog of laag) prijsniveau wordt be-
reikt. Indien deze percentuele afname van de snelheid daarentegen groot is, neigt de verdeling
naar een platykurtische vorm, waarbij de verdeling platter wordt en bijgevolg de kans op een ex-
treem prijsniveau relatief hoog is. In het geval dat de kansverdeling zich tussen beide gevallen
bevindt, wordt deze mesokurtisch genoemd. Indien echter de kans op een prijsdaling (respectieve-
lijk prijsstijging) onafhankelijk is van het prijsniveau wordt deze kansverdeling voorgesteld door
een vlakke lijn, vergelijkbaar met de kansverdeling in hoofdstuk 4 waarbij de kansverdeling 50/50
was voor beide prijsniveaus. Figuur 4.5 geeft de verschillende situaties grafisch weer.
0
0,05
0,1
0,15
0,2
0,25
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41
Ste
ad
y-s
tate
ka
nse
n
Prijsniveau
v=1 (vlak)
v=0,99 (platykur!sch)
v=0,9 (mesokur!sch)
v=0,8 (leptokur!sch)
Figuur 4.5: Mogelijke kansverdelingen voor het prijsniveau in functie van v
Ter illustratie wordt in figuur 4.6 een simulatie gemaakt van hoe het verloop van het prijsniveau
in de tijd er zou kunnen uitzien, voor twee verschillende waarden voor v. Uit deze figuur blijkt
duidelijk dat het gebruiken van een kleine factor v er toe leidt dat het prijsniveau zich over het
algemeen dicht bij de gemiddelde prijs bevindt. Tevens zijn eventuele extreme prijsniveaus slechts
van korte duur. Indien daarentegen een factor v gehanteerd wordt die zich dicht bij een bevindt,
dan komen vaker extreme prijsniveaus voor en kan het prijsniveau ook gedurende een langere tijd
deze extreme waarden aanhouden alvorens terug naar het gemiddelde prijsniveau te evolueren.
Merk op dat deze vaststellingen ook een belangrijke invloed hebben op de frequentie van de fluctu-
aties. Bovenstaande bespreking van de frequentie heeft betrekking op de korte-termijn volatiliteit
van het prijsniveau. Deze wordt bepaald door de grootte van α en β. De grootte van de factor
v heeft op haar beurt een grote invloed op de fluctuaties op middellange termijn. In figuur 4.6
is immers duidelijk te zien dat bij een hoge factor v, het prijsniveau zich grotere periodes boven
55

0
5
10
15
20
25
30
35
Pri
jsn
ive
au
Tijd
v = 0,8
v = 0,95
Figuur 4.6: Simulatie van de evolutie van het prijsniveau in de tijd voor verschillende waarden van v
of onder de gemiddelde prijs bevindt. Bij een lager factor v daarentegen fluctueert de prijs veel
sneller tussen een hoger dan gemiddeld en een lager dan gemiddeld prijsniveau.
Scenario’s
Op basis van de hierboven besproken parameters en hun invloed op het prijsverloop is het reeds
mogelijk een vrij omvangrijk aantal scenario’s te bekijken omtrent dit prijsverloop. Het zal in-
teressant zijn om de invloed die deze parameters hebben op het bestelbeleid te analyseren. Men
kan verwachten dat bij een hogere korte-termijn prijsvolatiliteit sneller een bestelling zal geplaatst
worden in de situatie waarbij het prijsniveau lager ligt dan het gemiddelde. Daarentegen zal eerder
afwachtend gehandeld worden indien het prijsniveau hoger ligt dan gemiddeld. Omwille van de
hoge volatiliteit is de kans op een prijsdaling dan immers relatief groot.
Ook de invloed van de factor v op het bestelbeleid kan tot op zekere hoogte voorspeld worden.
Zoals hierboven besproken werd, heeft een hoge waarde voor deze factor als gevolg dat het prijsni-
veau een lagere middellange-termijn frequentie vertoont en zich bijgevolg langere periodes boven,
respectievelijk onder, het gemiddelde prijsniveau bevindt. Bijgevolg kan verwacht worden dat het
prijsniveau aan belang zal inboeten wat betreft het bestelbeleid, en dus de voorraadkost de door-
slaggevende factor wordt. Een lage prijs zal nu immers minder aanzetten tot het onmiddellijk
bestellen van goederen aangezien de kans groot is dat de prijs op het volgende tijdstip nog steeds
laag zal zijn.
56

4.2.3 Volledige Markov-keten
Om zowel de vraagfluctuaties als de prijsfluctuaties in een model te kunnen vatten, worden beide
Markov-ketens, in overeenstemming met hoofdstuk 3, opnieuw gecombineerd tot een Markov-
keten met twee dimensies. Het aantal mogelijke toestanden zal bijgevolg gelijk zijn aan (C+1)·K,
waarbijC+1 enK het aantal mogelijke toestanden voorstellen van de twee afzonderlijke Markov-
ketens. De volledige toestandsruimte (S1, S2, ..., S(C+1)·K) wordt weergegeven in tabel 4.2.
Tabel 4.2: Volledige toestandsruimte van het uitgebreide model
Toestand Voorraadniveau Prijsniveau
S1 C P1
S2 C P2...
......
SK C PKSK+1 C − 1 P1
SK+2 C − 1 P2...
......
S(C+1)·K 0 PK
4.2.4 Markoviaans beslissingsproces
Het aantal mogelijk acties di zal in dit uitgebreid model een heel stuk hoger liggen in vergelijking
met hoofdstuk 3. In elke toestand zal opnieuw beslist moeten worden of er besteld wordt en
hoeveel er besteld zal worden. De maximale hoeveelheid goederen die kan besteld worden is
uiteraard gelijk aan het maximale voorraadniveauC. Deze maximale hoeveelheid zal tevens gelijk
zijn aan het aantal mogelijke bestelhoeveelheden (d2, d3, . . . , dC+1). De actie d1 komt opnieuw
overeen met de actie ’niets bestellen.’ Figuur 4.7 geeft de mogelijke acties grafisch weer. In deze
figuur wordt abstractie gemaakt van het prijsniveau. In welke toestand het systeem terecht komt
na het nemen van een bepaalde actie hangt opnieuw af van het al dan niet aanwezig zijn van vraag,
alsook de prijsevolutie. De invloed van de parameter p werd reeds besproken in figuur 3.5. De
lussen onderaan de figuur stellen een bestelling van een eenheid voor gecombineerd met vraag.
De zwarte pijlen stellen dan weer de mogelijke gevolgen voor van de actie ’niets bestellen’. De
afwezigheid van een lus boven het laagste voorraadniveau duidt er opnieuw op dat er in dit laagste
voorraadniveau sowieso moet besteld worden. In hoofdstuk 5 zal deze belangrijke assumptie
wegvallen.
57

C C − 1 . . . 2 1 0
Figuur 4.7: Mogelijke acties en de gevolgen
Transitiematrices
De transitiematrices voor elke mogelijke actie kunnen opnieuw opgesteld worden met behulp van
het Kronecker product van beide Markov-ketens. Deze methodologie is reeds uitvoerig beschreven
in sectie 3.2.3.
Kostmatrices
De kostmatrices zijn ook hier een combinatie van de voorraadkost per eenheid Ch en de aankoop-
kost. Deze laatste wordt nu gegeven door C0 + x · Pt waarbij x het aantal bestelde goederen
voorstelt en Pt het prijsniveau op het moment van bestellen (tijdstip t). Terwijl de voorraadkost
enkel afhankelijk is van het voorraadniveau, is de aankoopkost op haar beurt enkel afhankelijk van
de bestelhoeveelheid en het prijsniveau. Verder zijn deze kostmatrices eveneens zeer gelijkaardig
aan deze uit sectie 3.2.3.
4.3 Resultaten
In deze sectie zullen de belangrijkste resultaten besproken worden. In sectie 4.3.1 wordt eerst de
invloed van een van de dimensies van de Markov-keten, het prijsniveau, besproken. In sectie 4.3.2
wordt in overeenstemming met hoofdstuk 3 een vergelijking gemaakt tussen de verschillende op-
lossingsmethodes wat betreft enerzijds de benodigde CPU-tijd en anderzijds het aantal iteraties.
In secties 4.3.3, 4.3.4, 4.3.5 en 4.3.6 wordt vervolgens de invloed besproken van enkele modelva-
riabelen. Deze variabelen zijn respectievelijk de bestelkost, de disconteringsfactor, de vraag en de
prijsfluctuaties.
4.3.1 Invloed van de prijs op het bestelbeleid
Het verwachte resultaat van dit model is een bestelbeleid waarbij de bestelhoeveelheid afneemt
naarmate het prijsniveau of het voorraadniveau in waarde toeneemt. Indien het prijsniveau hoog
58

is zal de beslissingsnemer immers hopen op een prijsdaling in de toekomst en hierbij vrede ne-
men met een hogere gemiddelde bestelkost. Indien het aantal eenheden in voorraad hoog is zal de
beslissingsnemer eveneens minder bestellen aangezien dit de gemiddelde voorraadkost zou doen
toenemen. Indien we bijvoorbeeld zouden kiezen voor de parameters gegeven in tabel 4.3 verkrij-
gen we het bestelbeleid zoals weergegeven in figuur 4.8.
Tabel 4.3: Arbitrair gekozen parameters voor het oplossen van het uitgebreide model
Parameter Waarde Parameter Waarde
C 20 α = β 0, 3
K 20 d 0, 9
Ch 0, 1 p 0, 6
C0 20 z 0, 2
01
23
45
67
8910
11
101520253035404550556065707580859095100
0
2
4
6
8
10
12
PrijsniveauVoorraadniveau
Best
elho
evee
lhei
d
Figuur 4.8: Invloed van de het prijs- en voorraadniveau op het bestelbeleid
In figuur 4.8 is duidelijk de invloed van een aantal parameters te zien. Het wijzigen van de bestel-
hoeveelheid ten opzichte van respectievelijk het voorraad- en prijsniveau verloopt zoals verwacht;
er wordt meer besteld naarmate de voorraad bijna uitgeput is en de prijs relatief laag is. De drem-
pelwaarde waarbij niet langer besteld wordt, hangt af van een aantal factoren zoals de bestelkost,
de voorraadkost en de prijsfluctuaties (zowel amplitude als frequentie, zie sectie 4.2.2). Enkel
59

indien de voorraad uitgeput is, zal deze drempelwaarde afwezig zijn en zal steeds besteld worden,
onafhankelijk van deze factoren (zie figuur 4.9). Dit is namelijk een van de assumpties van dit
model, dit in tegenstelling tot hoofdstuk 5 waar de kost van verloren vraag zal geıntroduceerd
worden.
Elk voorraadniveau wordt gekenmerkt door een exponentiele functie met het prijsniveau als onaf-
hankelijke en de bestelhoeveelheid als afhankelijke variabele. In de hogere voorraadniveaus wordt
deze exponentiele functie echter steeds vroeger onderbroken omdat het in deze situatie mogelijk
is om af te wachten en te hopen dat het prijsniveau in de nabije toekomst lager komt te liggen.
Ook langs de tweede as is duidelijk een dalende functie waar te nemen met het voorraadniveau als
onafhankelijke variabele. Deze dalende curve is te wijten aan de invloed van een hogere voorraad-
kost. Bovendien wordt deze curve reeds bij een lagere bestelhoeveelheid afgebroken. De reden
hiervoor is de gezamenlijke invloed van enerzijds de voorraadkost en anderzijds de bestelkost. Zo
wordt bijvoorbeeld nooit slechts een eenheid besteld, tenzij de bestelkost C0 zeer klein wordt. Een
uitzondering hierbij is het laagste voorraadniveau aangezien dit een assumptie is in dit model (zie
figuur 4.9).
Merk op dat in figuur 4.8 in het overgrote deel van de toestanden geen goederen besteld worden.
Dit valt voor een groot deel te verklaren door de lage onzekerheid inherent aan dit model omwille
van de afwezigheid van een onzekere levertermijn. Indien het prijsniveau hoog is zal altijd gewacht
worden om te bestellen aangezien de kans op een prijsdaling reeel is en er geen enkel risico is dat
de voorraad uitgeput zal raken. Indien een levertermijn geıntroduceerd wordt is dit risico wel
aanwezig en zal de beslissingsnemer hierdoor sneller moeten handelen en dus ook bij hogere
prijsniveaus genoodzaakt zijn om een bestelling te plaatsen.
10 20 30 40 50 60 70 80 90 1000
2
4
6
8
10
12
Prijsniveau
best
elho
evee
lhei
d
10 20 30 40 50 60 70 80 90 1000
2
4
6
8
10
12
Prijsniveau
best
elho
evee
lhei
d
Figuur 4.9: Invloed van de prijs op het bestelbeleid in het laagste voorraadniveau
60

4.3.2 Vergelijking van de verschillende oplossingsmethodes
Tabel 4.4 geeft een overzicht van de efficientie van de verschillende oplossingsmethodes in het
oplossen van dit model. In de tabel wordt een vergelijking gemaakt van de benodigde CPU-tijd
voor het oplossen van een model met een 4 × 2, respectievelijk 20 × 20, toestandsruimte. De
oplossingsmethodes werden reeds besproken in sectie 2.2.
Tabel 4.4: Vergelijking van de verschillende oplossingsmethodes in een 4 × 2, respectievelijk 20 × 20toestandsruimte
(a) 4× 2
Oplossingsmethode Aantal iteraties CPU-tijd [ms]
Lineair programmeren n.v.t. 14
Policy iteration 3 1, 1
Policy iteration modified 7 3, 6
Value iteration 40 3, 1
Value iteration GS 48 12, 5
(b) 20× 20
Iteraties CPU-tijd [s]
n.v.t. 331, 02
5 0, 55
6 0, 79
48 4, 19
91 8, 92
Indien tabel 4.4 (a) vergeleken wordt met tabel 3.5 uit het vorige hoofdstuk, kan opgemerkt worden
dat dit model duidelijk meer iteraties en computertijd vergt, ondanks het gebruik van een identieke
toestandsruimte. Dit is een logisch gevolg van het groter aantal mogelijke acties die kunnen ge-
kozen worden. Er kan nu immers niet enkel in het laagste voorraadniveau besteld worden, noch
zijn de mogelijkheden beperkt tot het bestellen van twee of drie eenheden. De oplossingsmethode
die hier het minste nadeel van ondervindt blijkt policy iteration te zijn. Hoe snel de benodigde
CPU-tijd oploopt naarmate de toestandsruimte groter wordt hangt bij kleinere toestandsruimtes
hoofdzakelijk af van het resulterend bestelbeleid, meer bepaald van het aantal verschillende be-
stelhoeveelheden.
Indien de toestandsruimte uitgebreid wordt naar een 20 × 20 toestandsruimte (met 20 voorraad-
en prijsniveaus) kan duidelijker een onderscheid gemaakt worden tussen de verschillende oplos-
singsmethodes. Op basis van de resultaten uit tabel 4.4 (b) kunnen we besluiten dat het lineair
programmeren zoals verwacht geen goede oplossingsmethode is voor een model van dergelijke
omvang. De reden hiervoor is dat de simplex-methode (zie sectie 2.2) een weliswaar eenvoudig te
begrijpen maar weinig efficient algoritme is. Bovendien is deze oplossingsmethode niet specifiek
ontwikkeld voor het oplossen van Markoviaanse beslissingsprocessen, terwijl dit bij de vier andere
methodes wel het geval is. Verder blijkt policy iteration de beste oplossingsmethode te zijn voor
dit specifieke model. Reeds in hoofdstuk 2 werd vermeld dat policy iteration wellicht de beste
methode is indien met grote toestandsruimtes gewerkt wordt. Dit vermoeden wordt hier bevestigd
61

aangezien de benodigde CPU-tijd slechts weinig toeneemt met het aantal toestanden. Het is vooral
opvallend hoe weinig iteraties nodig zijn om een model van grote omvang op te lossen. Het lage
aantal iteraties is vermoedelijk dan ook de reden voor de trage toename van de benodigde CPU-
tijd. Dit in tegenstelling tot value iteration waar het aantal benodigde iteraties significant hoger
ligt, alsook de stijging in het aantal iteraties naarmate het aantal toestanden toeneemt.
In figuur 4.10 wordt een overzicht gegeven van de prestaties van de verschillende oplossingsme-
thodes in functie van het aantal toestanden. Hierbij blijkt duidelijk dat de tijd die value itera-
tion en het hiervan afgeleide Gauss-Seidel algoritme nodig hebben exponentieel gaat stijgen bij
grote toestandsruimtes. Bovendien lijkt het standaard value iteration algoritme iets efficienter dan
de Gauss-Seidel aanpassing, hoogstwaarschijnlijk omwille van het lagere aantal iteraties (zie ta-
bel 4.4). Merk op dat deze toestandsruimte al zeer groot moet zijn vooraleer het value iteration
algoritme significant slechter gaat presteren in vergelijking met policy iteration. Policy iteration
is op haar beurt iets efficienter dan het aangepaste policy iteration algoritme, maar dit verschil is
verwaarloosbaar.
0
50
100
150
200
250
300
350
400
450
Cp
u-
jd (
seco
nd
en
)
Groo"e toestandsruimte
Lineair programmeren
Policy itera on
Policy itera on modified
Value itera on
Value itera on GS
Figuur 4.10: Overzicht van de oplossingstijden van de verschillende oplossingsmethodes in functie van hetaantal toestanden
Merk op dat de figuur eindigt bij een 45× 44 toestandsruimte. De reden hiervoor is dat het model
vanaf dit kritieke punt onoplosbaar wordt op de computer beschreven in sectie 3.3.5, en dit met
elke beschreven oplossingsmethode. Omwille van de omvangrijke transitie- en kostmatrices wordt
op dit punt namelijk het volledige interne geheugen van deze computer gebruikt. Bij dit model zal
met andere woorden, indien het policy iteration algoritme gebruikt wordt, de benodigde CPU-tijd
geen enkel probleem vormen op voorwaarde dat het model opgelost wordt op een computernet-
werk dat voldoende intern geheugen bezit om de noodzakelijke bewerkingen te kunnen uitvoeren
62

op de omvangrijke matrices. Immers, hoe hoger dit interne geheugen, hoe hoger het kritieke punt
zal liggen wat betreft de grootte van de toestandsruimte. Niettemin is de gebruikte computer voor
deze masterproef krachtig genoeg om problemen van realistische omvang te kunnen oplossen. In-
dien het aantal voorraadniveaus hoger zou liggen dan het kritieke punt, kunnen immers een aantal
producteenheden worden samengevoegd tot een grotere producteenheid (’batch’).
4.3.3 Invloed van de bestelkost op het bestelbeleid
De invloed van de bestelkost C0 en de voorraadkost Ch op het bestelbeleid werd reeds uitgebreid
besproken in hoofdstuk 3. In figuur 4.11 worden deze resultaten wat betreft de bestelkost beves-
tigd voor dit uitgebreide model. Een hogere bestelkost resulteert logischerwijze in een hogere
maximale bestelhoeveelheid en tevens komen kleine bestelhoeveelheden veel minder voor. De
gemiddelde bestelhoeveelheid ligt met andere woorden hoger. De invloed van de voorraadkost is
niet weergegeven aangezien ook hier de resultaten voor de hand liggen. De overige parameters in
dit model werden arbitrair gekozen. In het vervolg van dit hoofdstuk zullen deze parameters steeds
onveranderd blijven, behalve diegene waarvan de invloed op het bestelbeleid bekeken wordt.
02
46
810
1214
16
102030405060708090100
0
5
10
15
20
PrijsniveauVoorraadniveau
Bes
telh
oeve
elhe
id
(a) Lage bestelkost
02
46
810
12
102030405060708090100
0
5
10
15
20
25
PrijsniveauVoorraadniveau
Bes
telh
oeve
elhe
id
(b) Hoge bestelkost
Figuur 4.11: Invloed van de bestelkost C0 op het bestelbeleid
4.3.4 Invloed van de disconteringsfactor op het bestelbeleid
Wanneer gewerkt wordt met een verdisconteerde kost zijn de resultaten steeds sterk afhankelijk
van de grootte van deze disconteringsfactor d. De waarde die dient gegeven te worden aan deze
factor, vormt een belangrijk onderwerp van discussie in de financiele wereld bij het nemen van
investeringsbeslissingen. Maar ook bij dit model speelt deze factor een belangrijke rol.
63

Een hogere disconteringsfactor heeft als gevolg dat de kosten minder zwaar gaan doorwegen naar-
mate deze zich meer in de toekomst bevinden. Bijgevolg kan verwacht worden dat als gevolg hier-
van de bestelhoeveelheid hoger zal liggen. Dit verhoogt weliswaar de voorraadkosten, maar deze
bevinden zich grotendeels in de toekomst. De bestelkost per eenheid, die op het huidige tijdstip
in rekening wordt gebracht, wordt dan weer kleiner. Hierdoor verkleint de totale verdisconteerde
kost. Bij een hogere disconteringsfactor zal dus ook sneller besteld worden; dit wil zeggen, star-
tend van een hoger voorraadniveau. In figuur 4.12 is duidelijk weergegeven hoe belangrijk een
juiste inschatting van deze factor d is.
02
46
810
1214
1618
102030405060708090100
0
5
10
15
20
25
PrijsniveauVoorraadniveau
Bes
telh
oeve
elhe
id
(a) d = 0.95
02
46
8
102030405060708090100
0
2
4
6
8
10
PrijsniveauVoorraadniveau
Be
ste
lho
eve
elh
eid
(b) d = 0.9
Figuur 4.12: Invloed van de disconteringsfactor d op het bestelbeleid
De waarde voor de disconteringsfactor die gebruikt moet worden hangt af van de specifieke situ-
atie van de onderneming, alsook van het verwachte tijdsinterval tussen twee bestellingen. Indien
twee opeenvolgende bestellingen sterker gespreid zijn in de tijd moet vanzelfsprekend een hogere
disconteringsfactor worden toegepast.
4.3.5 Invloed van de vraag op het bestelbeleid
Reeds eerder werd vermeld dat de tijd tussen twee opeenvolgende bestellingen geometrisch ver-
deeld is. Tevens wordt de kans op vraag voorgesteld door de parameter p. Een grotere kans op
vraag (een hogere p) zorgt er bijgevolg voor dat het gemiddelde tijdsinterval tussen twee opeen-
volgende bestellingen kleiner wordt. Men kan verwachten dat er hierdoor meer en sneller zal
besteld worden. De bestelde goederen zullen immers minder lang in voorraad blijven hetgeen de
voorraadkosten vermindert. Deze vermoedens worden bevestigd in figuur 4.13.
64

02
46
810
1214
1618
102030405060708090100
0
5
10
15
20
25
PrijsniveauVoorraadniveau
Bes
telh
oeve
elhe
id
(a) p = 0.6
02
46
810
1214
1618
2022
2426
102030405060708090100
0
10
20
30
PrijsniveauVoorraadniveau
Bes
telh
oeve
elhe
id
(b) p = 0.9
Figuur 4.13: Invloed van de kans op vraag op het bestelbeleid
4.3.6 Invloed van de prijsfluctuaties op het bestelbeleid
De verwachte invloed van de prijsfluctuaties op het bestelbeleid werd reeds besproken in sec-
tie 4.2.2. Deze prijsfluctuaties worden gekenmerkt door twee karakteristieke grootheden, de fre-
quentie en de amplitude. De frequentie is hier een uitdrukking voor de korte-termijn volatiliteit
van het prijsniveau en wordt beınvloedt door de grootte van α en β. In figuur 4.14 wordt de invloed
van deze volatiliteit op het bestelbeleid duidelijk weergegeven.
02
46
810
1214
16
102030405060708090100
0
5
10
15
20
PrijsniveauVoorraadniveau
Bes
telh
oeve
elhe
id
(a) a = b = 0.2
02
46
810
1214
1618
102030405060708090100
0
5
10
15
20
25
PrijsniveauVoorraadniveau
Bes
telh
oeve
elhe
id
(b) a = b = 0.4
Figuur 4.14: Invloed van de frequentie van de prijsfluctuaties op het bestelbeleid
Zoals verwacht zorgt een hogere prijsvolatiliteit (hogere α en β) er voor dat er sneller een bestel-
ling zal geplaatst worden bij een laag prijsniveau. De kans dat het prijsniveau opnieuw zal stijgen
65

is immers groot. Bovendien zal om dezelfde reden ook een grotere hoeveelheid besteld worden
indien het prijsniveau heel laag is. Merk ook op dat bij een lage prijsvolatiliteit geen kleine bestel-
lingen geplaatst worden en de drempel om te bestellen bovendien op een lager prijsniveau ligt. De
kleine kans op een prijsstijging weegt waarschijnlijk niet op tegen de hogere voorraadkost indien
vroegtijdig besteld wordt.
Indien de kansen α en β van elkaar verschillen wijzigt de kansverdeling van het prijsniveau (zie
figuur 4.4 op pagina 54). De gevolgen hiervan op het bestelbeleid zijn eenvoudig te voorspellen en
deze verwachte gevolgen worden bevestigd door de resultaten. Indien de kans op een prijsdaling
α groter is dan de kans op een prijsstijging β zal eerder afwachtend gehandeld worden. Indien de
kans op een prijsdaling α daarentegen kleiner is dan de kans op een prijsstijging β, zal veel sneller
gereageerd worden op een tijdelijk laag prijsniveau en zullen er grotere hoeveelheden besteld
worden in een dergelijke situatie. De kans dat het systeem zich in de toekomst nog in dit lage
prijsniveau zal bevinden is immers veel kleiner.
De invloed van de factor v valt ook te voorspellen. Ter herhaling, deze parameter bepaalt de
snelheid waarmee de kans op een prijsdaling, respectievelijk prijsstijging, afneemt naarmate de
prijs zich verder van het gemiddelde bevindt. Een hoge waarde voor v impliceert dat deze kansen
traag afnemen. Hieruit volgt dat de amplitude van de prijsfluctuaties groter wordt en er bijgevolg
meer extreme prijsniveaus worden bereikt. Bovendien heeft een hoge waarde voor v ook tot gevolg
dat het prijsniveau zich gedurende langere periodes in een hoog, respectievelijk laag, prijsniveau
zal bevinden. Een lage waarde voor v daarentegen heeft tot gevolg dat het prijsniveau fluctueert
dicht rond het lange-termijn gemiddelde prijsniveau. Bovendien zijn meer extreme prijs slechts
van kortere duur. In figuur 4.15 wordt de invloed van deze parameter op het bestelbeleid grafisch
weergegeven.
Zoals verwacht heeft een lage waarde voor de parameter v tot gevolg dat er grotere hoeveelheden
besteld worden indien het prijsniveau zeer laag is. De kans op een dergelijk prijsniveau is immers
kleiner. Wanneer de prijs zich echter rond het lange-termijn gemiddelde prijsniveau bevindt zal
net minder snel besteld wordt. De kans dat het systeem zich in de nabije toekomst opnieuw in
een prijsniveau dicht bij dit gemiddelde bevindt is immers groot, terwijl de kans dat een extreem
hoog prijsniveau bereikt en aangehouden wordt zeer klein is. De beslissingsnemer zal bijgevolg,
omwille van dit zeer kleine risico, afwachten en hopen op een prijsdaling.
66

02
46
810
1214
1618
102030405060708090100
0
5
10
15
20
25
PrijsniveauVoorraadniveau
Bes
telh
oeve
elhe
id
(a) v = 0.5
02
46
810
1214
1618
102030405060708090100
0
5
10
15
20
PrijsniveauVoorraadniveau
Bes
telh
oeve
elhe
id
(b) v = 0.8
Figuur 4.15: Invloed van de factor v op het bestelbeleid
67

Hoofdstuk 5
Model met een onzekere levertermijn
5.1 Inleiding
In dit hoofdstuk wordt het model uit hoofdstuk 4 verder uitgebreid door het laten vallen van een
belangrijke vereenvoudigende veronderstelling. Tot nu toe werd namelijk verondersteld dat elke
bestelling onmiddellijk geleverd werd, zonder enige onzekerheid wat betreft de levertermijn. Dit
had onder andere als gevolg dat er geen veiligheidsvoorraad werd aangelegd. Indien toch vroeger
werd besteld had dit louter tot doel om te profiteren van een tijdelijk laag prijsniveau. In dit hoofd-
stuk wordt dit model verder uitgebreid door middel van het introduceren van een onzekere ’lead
time’ of levertermijn. De onzekerheid wat betreft het tijdstip van levering heeft als gevolg dat er
voortaan rekening moet gehouden worden met een nieuwe kostencategorie, namelijk de ’kost van
verloren vraag’. De mogelijkheid bestaat nu immers om in een situatie terecht te komen waarbij
niet langer aan de vraag kan voldaan worden ten gevolge van een onverwacht lange levertermijn.
Zoals reeds vermeld in sectie 1.1 kan de totale voorraad worden opgesplitst in drie componenten
die elk hun eigen trade-offs met zich meebrengen. Een eerste component, de seizoensvoorraad,
wordt buiten beschouwing gelaten in deze masterproef. Een tweede component is de cyclische
voorraad en deze werd uitgebreid besproken in hoofdstuk 3 en 4. Deze component stelt de ge-
middelde hoeveelheid voorraad voor die nodig is om aan de vraag te voldoen. Waar deze vraag in
het EOQ-model deterministisch is, wordt in deze masterproef evenwel gewerkt met een stochasti-
sche, fluctuerende vraag. De derde component is de veiligheidsvoorraad. Deze wordt gedefinieerd
als de voorraad die aangehouden wordt om te kunnen voldoen aan een vraag die groter is dan de
vraagvoorspelling voor een gegeven periode [2, Hoofdstuk 11]. Deze component is nog niet be-
sproken in de eerste twee modellen. De levertermijn werd immers verondersteld gelijk te zijn aan
nul en bijgevolg kon steeds aan de vraag voldaan worden. Er was dus geen veiligheidsvoorraad
nodig, noch een kost van verloren vraag. In dit derde model wordt gewerkt met een variabele
68

levertermijn en is er bovendien onzekerheid omtrent de hoeveelheid goederen die zullen verkocht
worden gedurende de tijd dat een bestelling geplaatst maar nog niet geleverd is. De onzekerheid
wat betreft de vraag tijdens de levertermijn is een combinatie van de onzekerheid wat betreft ener-
zijds de lengte van de levertermijn en anderzijds de vraag per tijdseenheid. De kansverdeling
van de vraag gedurende de levertermijn wordt immers gegeven door de convolutie (het ’optellen’)
van de kansverdeling van de vraag per tijdseenheid en de kansverdeling van de levertermijn [2].
Het aanhouden van een veiligheidsvoorraad is bijgevolg noodzakelijk om een onverwacht lange
levertermijn te kunnen overbruggen en ondanks de onzekerheid een bevredigend service level te
bereiken. De bijkomende trade-off in deze situatie is immers de afweging tussen een hogere voor-
raadkost en het risico dat er niet aan de vraag kan voldaan worden. Dit risico wordt voorgesteld
door de kost van verloren vraag.
De grootte van deze veiligheidsvoorraad zal afhangen van twee factoren [2, Hoofdstuk 3]. Ten
eerste is deze positief afhankelijk van de onzekerheid in verband met zowel vraag als aanbod.
Wat betreft de vraag is bijgevolg de grootte van p belangrijk. De onzekerheid in het aanbod
heeft dan weer betrekking op de variabele levertermijn. Een bedrijf moet met andere woorden in
staat zijn om om te gaan met een ongewoon hoge vraag of een ongewoon lange levertermijn. De
tweede factor die van belang is bij het bepalen van de veiligheidsvoorraad is het belang voor de
onderneming van de continue beschikbaarheid van de goederen in kwestie. Dit belang is op zijn
beurt impliciet aanwezig in de kost van verloren vraag aangezien een hogere kost ertoe zal leiden
dat de goederen vroeger besteld worden, hetgeen leidt tot een hogere veiligheidsvoorraad.
In overeenstemming met hoofdstukken 3 en 4 zal in sectie 5.2 de modellering van de betreffende
probleemstelling worden uitgelegd. Hierbij zullen enkel de aanpassingen en uitbreidingen ten op-
zichte van hoofdstuk 4 aan bod komen. Vervolgens zullen in sectie 5.3 de belangrijkste resultaten
worden voorgesteld.
5.2 Model
In sectie 5.2.1 wordt uitgelegd hoe een onzekere levertermijn kan gemodelleerd worden aan de
hand van een Markov-keten en Markoviaans beslissingsproces. In sectie 5.2.2 wordt vervolgens
de kost van verloren vraag verder uitgediept.
De relevante parameters, gegeven in de tabellen 3.1 en 4.1 worden verder uitgebreid met een aantal
nieuwe parameters. Deze worden weergegeven in tabel 5.1 en uitgebreid besproken in de volgende
secties van dit hoofdstuk.
69

Tabel 5.1: Overzicht van de gebruikte variabelen en parameters
Weergave Uitleg
CV Kost van verloren vraagκ Kans op leveringκ 1− kans op leveringL Levertermijn
5.2.1 Levertermijn
In een realistische markt worden bedrijven steeds geconfronteerd met een bepaalde lead time, ook
wel levertermijn of doorlooptijd genoemd. Deze levertermijn wordt hier gedefinieerd als de totale
tijd tussen het verzoek om een bepaalde hoeveelheid goederen te leveren (de bestelling), en de
feitelijke levering. Bovendien is de grootte van deze levertermijn vaak onzeker en wordt deze
gemodelleerd aan de hand van een kansverdeling. In figuur 1.4 werd reeds een illustratie gegeven
van deze situatie, zij het met een continue in plaats van discrete vraag.
In deze masterproef wordt gekozen om deze onzekere levertermijn voor te stellen met behulp
van de parameter ’kappa’, voorgesteld door het symbool ’κ’. κ wordt gedefinieerd als de kans
op levering op een gegeven tijdstip indien in het verleden een bestelling geplaatst is. 1 − κ is
bijgevolg de kans dat de goederen nog niet geleverd worden. In dit geval is er opnieuw een kans
κ dat er geleverd zal worden op het volgende tijdstip. Het gevolg van deze methode is dat de
kansverdeling van deze levertermijn een exponentieel dalend verloop heeft. Figuur 5.1 illustreert
deze kansverdeling voor twee mogelijke waarden van κ. Op de figuur is ook de gemiddelde
levertermijn voor beide gevallen in het rood aangegeven. Indien κ gelijk aan een gekozen wordt,
bekomen we identiek hetzelfde model als in hoofdstuk 4. De levertermijn is dan immers gelijk
aan nul.
Aangezien het in de Markov-keten uit sectie 4.2.1 onmogelijk is om bij te houden of een bestelling
al dan niet geleverd is, is het noodzakelijk nog een extra dimensie toe te voegen aan de bestaande
Markov-keten, naast het voorraadniveau en het prijsniveau. Deze extra dimensie geeft aan of er
al dan niet een bestelling geplaatst maar nog niet geleverd is, en tevens hoeveel goederen er exact
besteld zijn. Indien er dus een bestelling geplaatst wordt maar er niet onmiddellijk geleverd wordt
(met kans 1 − κ), dan komt het systeem terecht in deze extra dimensie. In welke toestand het
systeem exact terechtkomt, hangt af van de bestelhoeveelheid en vanzelfsprekend ook nog steeds
van de kansen α, β en p. Figuur 5.2 illustreert deze extra dimensie voor het voorraadniveau
N . Indien bijvoorbeeld actie d2 wordt gekozen en er is noch vraag noch een verandering in het
prijsniveau, dan zal het systeem zich met kans 1 − κ naar toestand Nb bewegen. Indien actie d3
70

0,0%
5,0%
10,0%
15,0%
20,0%
25,0%
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49
Tijd
Kappa = 0.1
Kappa = 0.2
Figuur 5.1: Kansverdeling van de levertermijn en de gemiddelde levertermijn bij verschillende waardenvoor κ
gekozen wordt, dan zal het systeem zich met kans 1 − κ naar toestand Nc bewegen, enzovoort.
Indien echter de bestelling onmiddellijk geleverd wordt (met kans κ), dan zal deze extra dimensie
niet gebruikt worden maar zal het systeem direct in een toestand terechtkomen met een hoger
voorraadniveau zoals in hoofdstuk 4 het geval was.
N Nb Nc Nd1− κ(d2)
1− κ(d3)
1− κ(d4)
Figuur 5.2: Het introduceren van een extra dimensie in voorraadniveau N met als doel het modelleren vaneen variabele levertermijn
Indien het systeem zich op tijdstip t bevindt in een van deze toestanden die behoren tot de extra
dimensie, zal het systeem zich op tijdstip t + 1 gedragen zoals in hoofdstuk 4; dit wil zeggen
zolang de bestelling niet geleverd wordt. Wel wordt er verondersteld dat in de situatie waarbij reeds
besteld is, er geen tweede bestelling kan geplaatst worden. Indien reeds een bestelling onderweg is
zal er dus steeds gekozen worden voor actie d1, ’niets bestellen’. Op het moment dat de bestelling
geleverd wordt, keert het systeem terug naar zijn ’eerste dimensie’, wordt de bestelhoeveelheid
bij het voorraadniveau opgeteld en kan er opnieuw besteld worden. In figuur 5.3 wordt dit model
geıllustreerd aan de hand van een voorbeeld. In deze figuur wordt verondersteld dat het systeem
zich bevindt in een toestand waarbij twee eenheden in voorraad zijn en actie d3 gekozen wordt;
71

er worden bijgevolg twee eenheden besteld. Om het geheel overzichtelijk te houden zijn enkel
de overgangskansen vanuit voorraadniveau 2 en lager weergegeven. De blauwe pijlen stellen de
mogelijke overgangen voor vanuit voorraadniveau 2 indien actie d3 wordt gekozen. De rode pijlen
stellen de overgangskansen voor indien geen actie wordt ondernomen. De groene pijlen stellen de
overgangskansen voor vanuit toestand 2c. Aangezien er twee eenheden besteld zijn (actie d3) kan
het voorraadniveau stijgen met een of met twee eenheden, afhankelijk van het al dan niet aanwezig
zijn van vraag. De overgangen vanuit toestanden 1c en 0c zijn slechts gedeeltelijk weergegeven om
de figuur niet te overladen. Deze toestanden gedragen zich echter op dezelfde manier als toestand
2c.
4 3 2 1 0
2c 1c 0c
p p
p ∗ κ
p · κ p · κ
p · κp · κ
p · κ
p · κp · κ
1− p 1− p 1
p · κ p · κ p · κ
Figuur 5.3: Illustratie van het model met levertermijn aan de hand van een voorbeeld
In bovenstaande redenering werd abstractie gemaakt van het prijsniveau. Deze dimensie moet
uiteraard ook in rekening gebracht worden bij het opstellen van de volledige Markov-keten en het
volledige Markoviaans beslissingsproces. Om praktische redenen werd de prijsdimensie echter
genegeerd in deze paragraaf aangezien dit de figuren onleesbaar zou maken. Bovendien heeft de
prijs geen enkele invloed op de specifieke dynamiek van bovenstaand model met levertermijn.
Een belangrijk gevolg van het introduceren van een variabele levertermijn is dat de toestands-
ruimte waarmee gewerkt wordt exponentieel vergroot. Voor elk voorraadniveau worden immers
nieuwe toestanden gecreeerd die weergeven hoeveel goederen reeds besteld zijn. De tijd die no-
dig is om dit Markoviaans beslissingsproces op te lossen zal naar alle waarschijnlijkheid dan ook
exponentieel stijgen. Dit zou deels verholpen kunnen worden door te veronderstellen dat er enkel
in welbepaalde lotgroottes kan besteld worden.
72

5.2.2 De kost van verloren vraag
Indien de levering onverwacht lang op zich laat wachten, is het mogelijk dat de voorraad uitgeput
raakt en er niet meer aan de vraag kan voldaan worden. In dit geval gaat er niet alleen omzet
verloren, een opportuniteitskost, maar bestaat ook het risico dat de reputatie van het bedrijf aan-
getast wordt en de klant overstapt naar een concurrent. Deze kost is bijgevolg zeer moeilijk in
te schatten. In het model uit deze masterproef wordt verondersteld dat de vraag en dus de omzet
verloren gaat. Er is met andere woorden geen mogelijkheid om de goederen op een later tijdstip
te leveren (’backlogging’).
Indien het systeem zich in het laagste voorraadniveau bevindt en met andere woorden de voorraad
uitgeput is, dan kan niet langer voldaan worden aan een eventuele vraag. In tegenstelling tot in
hoofdstukken 3 en 4 kan dit tevens niet vermeden worden door het plaatsen van een bestelling op
ditzelfde tijdstip. Er moet met andere woorden een kost van verloren vraag CV geıntroduceerd
worden. Dit heeft ook als gevolg dat, in tegenstelling tot de vorige hoofdstukken, de mogelijkheid
om niet te bestellen op dit laagste voorraadniveau wordt toegevoegd.
Technisch wordt deze aanpassing doorgevoerd door het introduceren van een extra fictief voor-
raadniveau −1. Met behulp van dit fictieve niveau kan de exacte gesimuleerde kost van verloren
vraag berekend worden in plaats van enkel de verwachte kost. Indien de voorraad uitgeput is zorgt
een vraag op tijdstip t ervoor dat het systeem zich op tijdstip t + 1 in dit fictieve voorraadniveau
bevindt. Hierbij zal op tijdstip t+ 1 een kost CV aangerekend worden op een wijze vergelijkbaar
met het aanrekenen van de voorraadkost Ch in een hoger voorraadniveau. Met andere woorden,
deze kost wordt aangerekend onafhankelijk van de actie die wordt ondernomen. Vervolgens wordt
dit fictieve niveau op exact dezelfde manier behandeld als in de situatie waarbij het voorraadni-
veau gelijk is aan nul. Op tijdstip t + 1 zal het systeem zich dan ook terug in het voorraadniveau
gelijk aan nul bevinden, tenzij er opnieuw vraag is. Figuur 5.4 geeft de Markov-keten die deze
constructie modelleert grafisch weer.
C . . . 2 1 0 −1p p p p
p
1− p1− p 1− p 1− p 1− p p
Figuur 5.4: Het introduceren van een fictief voorraadniveau −1 in de Markov-keten
Belangrijk om te vermelden is dat dit fictieve voorraadniveau zowel van toepassing is op de ’nor-
male’ Markov-keten als op de extra dimensie die geıntroduceerd werd om de lead time te kunnen
modelleren.
73

Wat betreft de transitiematrix zullen de rijen die de laagste twee voorraadniveaus −1 en 0 voor-
stellen identiek zijn. De dynamiek in deze twee voorraadniveaus is immers dezelfde aangezien
er geen goederen in voorraad zijn. Enkel de corresponderende rijen in de kostmatrices zullen
van elkaar verschillen, omdat bij het voorraadniveau −1 een kost van verloren vraag aangerekend
wordt.
5.3 Resultaten
In deze sectie zullen de belangrijkste resultaten besproken worden. Hierbij ligt de focus op het
verschil van dit model met levertermijn ten opzichte van het model uit hoofdstuk 4. In sectie 5.3.1
worden eerst de gevolgen besproken van het invoeren van een onzekere levertermijn in het be-
staande model. In sectie 5.3.2 wordt vervolgens de invloed besproken van de kost van verloren
vraag op het bestelbeleid. In sectie 5.3.3 ten slotte wordt in overeenstemming met hoofdstuk-
ken 3 en 4 een vergelijking gemaakt tussen de verschillende oplossingsmethodes wat betreft de
efficientie in het oplossen van dit model.
5.3.1 Gevolgen van het invoeren van een onzekere levertermijn
De aanwezigheid van een onzekere levertermijn heeft tot gevolg dat de beslissingsnemer een vei-
ligheidsvoorraad zal aanleggen. Deze veiligheidsvoorraad moet het risico verminderen op een
voorraadtekort en bijgevolg vermijden dat er al te veel omzet verloren gaat. In figuur 5.5 wordt
een vergelijking gemaakt tussen het model zonder levertermijn (dit komt overeen met een kans op
levering κ gelijk aan een) en een model met een onzekere levertermijn. Verder wordt de invloed
weergegeven van de factor κ op het bestelbeleid. Merk op dat het fictieve voorraadniveau −1 niet
werd weergegeven op deze figuur aangezien deze geen praktische betekenis heeft. Bovendien is
het bestelbeleid in dit fictieve niveau identiek aan het bestelbeleid in het laagste voorraadniveau
(nul) op figuur 5.5. Ook de extra, derde dimensie wordt logischerwijze niet weergegeven op de
figuur.
Merk op dat de toestandsruimte in figuur 5.5 een lager aantal prijsniveaus bevat in vergelijking met
hoofdstuk 4. De reden hiervoor is de explosie van de toestandsruimte omwille van de ingevoerde
extra dimensie, en daaruit volgend de sterke stijging in de oplossingstijden (zie sectie 5.3.3).
Op de figuur is duidelijk te zien dat het invoeren van een onzekere levertermijn ervoor zorgt dat
er veel sneller en dus reeds bij een hoger voorraadniveau een bestelling geplaatst wordt. Boven-
dien is de bestelde hoeveelheid in elke mogelijke toestand groter. Hieruit volgt evenwel dat de
gemiddelde voorraad hoger ligt en bijgevolg ook de voorraadkosten. Een onzekere levertermijn
brengt met andere woorden altijd een hogere kost met zich mee net zoals elke andere vorm van
74

01
23
45
67
8
102030405060708090100
0
2
4
6
8
10
12
PrijsniveauVoorraadniveau
Best
elho
evee
lhei
d
(a) Model zonder levertermijn (κ = 1)
01
23
45
67
8910
102030405060708090100
0
2
4
6
8
10
12
PrijsniveauVoorraadniveau
Best
elho
evee
lhei
d
(b) Model met onzekere levertermijn (κ = 0.7)
01
23
45
67
8910
1112
102030405060708090100
0
5
10
15
PrijsniveauVoorraadniveau
Best
elho
evee
lhei
d
(c) Model met onzekere levertermijn (κ = 0.3)
01
23
45
67
8910
1112
13
102030405060708090100
0
5
10
15
PrijsniveauVoorraadniveau
Best
elho
evee
lhei
d
(d) Model met onzekere levertermijn (κ = 0.1)
Figuur 5.5: Effect van het invoeren van een onzekere levertermijn op het bestelbeleid
onzekerheid. Het verlagen van deze onzekerheid leidt veelal dan ook tot grotere kostenreducties
in vergelijking met het verlagen van de gemiddelde levertermijn. In deze masterproef worden
deze twee eigenschappen echter beiden bepaald door een enkele parameter, namelijk de kans op
levering κ. Hoe lager deze kans op levering per tijdseenheid is, hoe sneller er besteld wordt en
hoe groter de aangelegde veiligheidsvoorraad. Dit laatste kan worden afgeleid uit de grotere be-
stelhoeveelheden in figuur 5.5 (c) en (d).
Opvallend zijn de gevolgen van een zeer kleine κ in deze specifieke situatie. In figuur 5.5 (d) wordt
een kans op levering gelijk aan 0, 1 gehanteerd. Dit komt overeen met een gemiddelde levertermijn
van ongeveer 10, 5 tijdseenheden (zie figuur 5.1). In deze situatie is de kans op levering zodanig
klein dat er, wanneer de prijs hoog is, zelfs in het laagste voorraadniveau geen goederen besteld
wordt. Op dit moment is vermoedelijk de kans dat een bestelling op het laatste moment nog
spoedig geleverd wordt zo klein geworden, dat de iets lagere kost van verloren vraag (door nu te
bestellen in plaats van te wachten op een lager prijsniveau) niet opweegt tegen de hogere prijs die
moet betaald worden voor de goederen. Deze waarneming hangt met andere woorden ook sterk af
75

van de aard van de prijsfluctuaties.
In figuur 5.6 wordt de invloed van de factor κ op een alternatieve manier weergegeven door middel
van de ’besteldrempel’. Deze besteldrempel geeft weer hoe snel er besteld wordt in het laagste
prijsniveau of met andere woorden hoever het voorraadniveau moet gedaald zijn alvorens een be-
stelling geplaatst wordt. Bij een grotere kans op levering is zoals reeds besproken de levertermijn
korter en de benodigde veiligheidsvoorraad lager. Bijgevolg ligt ook de besteldrempel lager. Het
is in deze situatie immers niet nodig om de hogere voorraadkosten te torsen, aangezien door de
hoge kans op levering de kans op een voorraadtekort zeer gering is.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 10
2
4
6
8
10
12
Kans op levering (kappa)
Bes
teld
rem
pel(
Voor
raad
nive
au)
Figuur 5.6: De invloed van de kans op levering κ op de ’besteldrempel’
Een gelijkaardige grafiek zou kunnen gemaakt worden waarbij de besteldrempel wordt weergege-
ven wat betreft het prijsniveau in plaats van het voorraadniveau. Aangezien een hogere kans op
levering het risico vermindert op een voorraadtekort zal het vaak voordelig zijn om te wachten op
een lager prijsniveau.
5.3.2 Invloed van de kost van verloren vraag op het bestelbeleid
Zoals reeds eerder vermeld is de kost van verloren vraag bij een voorraadtekort een verzameling
van verscheidene factoren, zoals de verloren omzet en een geschaadde reputatie. De grootte van
deze kost is vaak zeer moeilijk in te schatten en kan zeer hoog oplopen. Bovendien vormt een
continue beschikbaarheid van goederen vaak een competitief voordeel ten opzichte van concur-
renten. Soms is dit zelfs contractueel vastgelegd, bijvoorbeeld bij belangrijke reserveonderdelen.
In figuur 5.7 is duidelijk te zien hoe groot de invloed is van deze kost op het bestelbeleid. Dit heeft
bijgevolg een grote impact op de kosten verbonden aan het voorraadbeheer van de onderneming.
Het is dan ook van vitaal belang om een goede schatting te maken van deze kost, specifiek voor
76

de betrokken onderneming.
01
23
45
67
89
102030405060708090100
0
2
4
6
8
10
12
PrijsniveauVoorraadniveau
Bes
telh
oeve
elhe
id
(a) Lage kost van verloren vraag (Cv = 100)
01
23
45
67
8910
1112
13
102030405060708090100
0
5
10
15
PrijsniveauVoorraadniveau
Bes
telh
oeve
elhe
id(b) Hoge kost van verloren vraag (Cv = 1000)
Figuur 5.7: Invloed van de kost van verloren vraag Cv op het bestelbeleid
In figuur 5.7 (a) zien we opnieuw de situatie waarbij, bij een hoge prijs, zelfs in het laagste voor-
raadniveau geen bestelling geplaatst worden. De kost van verloren vraag is immers zo klein dat
deze niet opweegt tegen de hoge prijs die moet betaald worden voor de goederen. In figuur 5.7 (b)
daarentegen is deze kost zodanig hoog dat er zelfs een bestelling geplaatst wordt bij een zeer hoge
prijs en niet enkel in het laagste voorraadniveau. Hier wordt een voorraadtekort ten allen tijde
vermeden. De combinatie van een lage kans op levering met een hoge kost van verloren vraag
versterkt dit effect nog verder (zie figuur 5.8).
01
23
45
67
8910
1112
13
102030405060708090100
0
5
10
15
PrijsniveauVoorraadniveau
Beste
lhoev
eelhe
id
Figuur 5.8: Gevolgen op het bestelbeleid van de combinatie van een hoge kost van verloren vraag en eenlage kans op levering
77

5.3.3 Vergelijking van de verschillende oplossingsmethodes
In sectie 4.3.2 werd reeds vermeld dat de oplosbaarheid van het model zich beperkt tot een 45× 44
toestandsruimte en dus tot ongeveer 1980 verschillende toestanden. Het invoeren van een onzekere
levertermijn heeft echter als gevolg dat de Markov-keten een extra, derde dimensie bevat. Indien
het modelC+2 verschillende voorraadniveaus bevat (inclusief voorraadniveaus−1 en 0) betekent
dit dat er maximaal C eenheden kunnen besteld worden. Bijgevolg wordt het aantal toestanden
met C vermenigvuldigd. Dit heeft tot gevolg dat de vermelde computer nog slechts een model kan
oplossen met bijvoorbeeld 15 voorraadniveaus en 10 prijsniveaus. Het aantal toestanden wordt
dan: 15× 13× 10 = 1950 toestanden. Indien het aantal voorraadniveaus verlaagd wordt (bijvoor-
beeld door meerdere eenheden samen te nemen in batches) kan het aantal prijsniveaus evenwel
sterk verhoogd worden. Omwille van de extra dimensie is het immers een verhoging van het
aantal voorraadniveaus die leidt tot de grootste explosie van de toestandsruimte.
In figuur 5.9 wordt een vergelijking gemaakt tussen de verschillende oplossingsmethodes waarbij
de benodigde CPU-tijd wordt uitgezet ten opzichte van het aantal toestanden (inclusief de extra
dimensie).
0,0
50,0
100,0
150,0
200,0
250,0
300,0
350,0
400,0
450,0
500,0
0 500 1000 1500 2000 2500
CP
U-
jd (
seco
nd
en
)
Groo"e toestandsruimte
Lineair programmeren
Policy itera on
Policy itera on modified
Value itera on
Value itera on GS
Figuur 5.9: Overzicht van de oplossingstijden van de verschillende oplossingsmethodes in functie van hetaantal toestanden
Wanneer deze figuur vergeleken wordt met figuur 4.10 uit hoofdstuk 4, dan zijn beide figuren
bijna volledig identiek. Er kunnen twee kleine verschillen opgemerkt worden. Ten eerste blijkt
de efficientie van het Gauss-Seidel value iteration algoritme bij grote toestandsruimtes een stuk
lager te liggen in vergelijking met het standaard value iteration algoritme. In hoofdstuk 4 lagen
deze verhoudingen nog omgekeerd. Ten tweede blijkt het aangepaste policy iteration algoritme de
78

meest efficiente oplossingsmethode voor dit model, terwijl dit in hoofdstuk 4 nog het standaard
policy iteration algoritme was. De verschillen tussen beide blijven echter verwaarloosbaar.
Merk op dat de grootste toestandsruimte uit figuur 5.9 slechts overeenkomt met een 15 × 13 toe-
standsruimte indien de extra dimensie wordt weggelaten. Om een model van realistische omvang
te kunnen oplossen zal bijgevolg gebruik moeten gemaakt worden van een krachtiger computer-
netwerk.
79

Conclusies en verder onderzoek
Algemeen besluit
Het doel van deze masterproef betrof het uitwerken en analyseren van een wiskundig model voor
voorraadbeheer, op maat van een specifieke bedrijfssituatie die nog niet als dusdanig werd on-
derzocht in de bestaande literatuur. De concrete uitdaging die in deze masterproef werd aange-
gaan, was het integreren van marktfluctuaties in een wiskundig model. In het bijzonder werd
een voorraadbeheer-model bestudeerd waarbij het aankoopgedrag niet enkel afhankelijk is van
een fluctuerend voorraadniveau, maar ook van een fluctuerende marktprijs. Merk op dat deze
fluctuaties betrekking hebben op korte- of middellange-termijn fluctuaties rond een lange-termijn
gemiddelde. Het model is bijgevolg niet van toepassing op continu in prijs dalende of stijgende
goederen, zoals bijvoorbeeld hightech producten in de IT sector. Lange-termijn-fluctuaties (con-
junctuur) vallen eveneens buiten het bereik van het model. Het doel was vervolgens het bepa-
len van een optimaal bestelbeleid waarbij de lange-termijn verdisconteerde kost geminimaliseerd
wordt. De keuze voor een verdisconteerde kost in plaats van een gemiddelde kost als doelfunc-
tie impliceert dat het model hoofdzakelijk toepasbaar is op producten waarbij zowel vraag- als
prijswijzigingen zich op de middellange termijn voordoen.
De vraagfluctuaties werden gemodelleerd op basis van een geometrische verdeling; meer bepaald
de tijd tussen twee opeenvolgende inkomende bestellingen is geometrisch verdeeld. Dit houdt in
dat, op basis van een kansverdeling, de kans op vraag op elk tijdstip gelijk is aan een of afwezig is.
De prijsfluctuaties werden zodanig gemodelleerd, dat zowel de kansverdeling van het prijsniveau
als de frequentie en de amplitude van de fluctuaties konden aangepast worden. Hierdoor was het
mogelijk verscheidene scenario’s te bekijken wat betreft deze prijsfluctuaties.
De beschouwde probleemstelling werd gemodelleerd met behulp van de theorie omtrent Markov-
ketens en Markoviaanse beslissingsprocessen. Ten eerste werden de prijs- en de voorraadfluctu-
aties gezamenlijk voorgesteld door middel van een discrete, stationaire Markov-keten met twee
dimensies. Dit impliceert een systeem dat zich op elk tijdstip in een bepaalde toestand kan bevin-
den, genomen uit een eindige verzameling van mogelijke toestanden. Elke toestand stelt hierbij de
80

combinatie voor van een welbepaald voorraad- en prijsniveau. Deze Markov-keten werd vervol-
gens voorgesteld door een transitie- of overgangsmatrix die de kansen weergeeft dat het systeem
in een tijdseenheid overgaat van de ene naar de andere toestand. Ten tweede werd de overgang
gemaakt naar een Markoviaans beslissingsproces door het introduceren van een aantal mogelijke
acties. Hierbij kan een beslissingsnemer een hoeveelheid goederen bestellen en bijgevolg de over-
gangskansen tussen twee toestanden beınvloeden. Op basis hiervan werd een transitiematrix op-
gesteld voor elke mogelijke actie. Bovendien werden ook kostmatrices opgesteld die de kosten
weergeven die gepaard gaan met het plaatsen van een bestelling (bestelkost) of die inherent ge-
bonden zijn aan een bepaalde toestand (voorraadkost). Op basis van beide categorieen matrices
kon het model vervolgens opgelost worden en kon een optimaal bestelbeleid berekend worden
waarbij de lange-termijn verdisconteerde kost geminimaliseerd werd. Dit bestelbeleid geeft in
elke toestand weer of er al dan niet besteld moet worden, alsook de optimale bestelhoeveelheid.
Het model in deze masterproef werd, om praktische redenen, stapsgewijs opgebouwd, waarbij in
elk hoofdstuk de toestandsruimte werd vergroot en/of een aantal vereenvoudigende veronderstel-
lingen werden weggelaten. Het laatste model introduceerde een onzekere levertermijn hetgeen
leidde tot een meer realistische voorstelling van de werkelijkheid. Technisch betekende deze aan-
passing dat er een extra dimensie werd toegevoegd aan de Markov-keten. Dit leidde tot een explo-
sie van de toestandsruimte hetgeen de oplosbaarheid van het model in negatieve zin beınvloedde.
Bovendien werd in dit laatste model een kost van verloren vraag geıntroduceerd. Deze kost is
een weergave van, onder andere, de verloren omzet en geschaadde reputatie als gevolg van een
voorraadtekort.
Het voorraadbeheer is een onderzoeksgebied waarin al decennia lang onderzoek wordt verricht.
Aangezien de wetten van het voorraadbeheer vrij logisch in elkaar zitten, werden er in deze mas-
terproef dan ook geen baanbrekende resultaten verwacht. Het doel van deze masterproef was
echter niet het ontdekken van nieuwe wetmatigheden, maar eerder het ontwikkelen van een model
dat toepasbaar is op een specifieke bedrijfssituatie die nog niet besproken werd in de bestaande
literatuur. In dit geval betreft dit het introduceren van prijsfluctuaties. Bovendien hangen de re-
sultaten sterk af van de specifieke veronderstellingen die gemaakt worden wat betreft de waarden
voor de relevante parameters en variabelen. Een kleine verandering in bepaalde parameters zoals
de disconteringsfactor, de prijsfluctuaties, de vraag, de bestelkost etc. heeft vaak een grote invloed
op de uitkomst van het model (het bestelbeleid). Deze observatie onderstreept het belang van
een model op maat voor elke onderneming. Het gebruik van een klassiek model kan immers een
compleet inefficient bestelbeleid tot gevolg hebben en bijgevolg leiden tot een sterke verhoging
van de kosten verbonden aan het voorraadbeheer van de onderneming. Het is dan ook van vitaal
belang om een goede schatting te maken van deze parameters, specifiek voor de betrokken onder-
81

neming. In deze masterproef werd dus getracht een bijdrage te leveren aan het voorraadbeheer
door het ontwikkelen van een model voor een specifieke situatie die nog niet was onderzocht in de
bestaande literatuur. Bovendien is ook de gebruikte methodiek nog weinig gebruikt in dit onder-
zoeksgebied. Elk bedrijf waarvan hun situatie overeenkomt met de veronderstellingen gemaakt in
deze masterproef, zou dit model kunnen gebruiken als basis voor het uitstippelen van een optimaal
bestelbeleid. Het voorgesteld model laat vervolgens een grondige analyse toe van de impact op
het bestelbeleid van een uitgebreid aantal parameters en variabelen.
Doorheen deze masterproef werd steeds een vergelijking gemaakt tussen de verscheidene op-
lossingsmethodes die ontwikkeld zijn voor het oplossen van een Markoviaans beslissingsproces.
Hieruit blijkt dat het policy iteration algoritme, of een aangepaste versie van dit algoritme, steeds
de beste resultaten kan voorleggen in een dergelijk grote toestandsruimte. Het value iteration al-
goritme is niettemin ook in staat om het model uit deze masterproef in korte tijd op te lossen. Het
formuleren van het betreffende probleem als een lineair programmeringsprobleem is daarentegen
niet aangewezen. Bovendien kan gesteld worden dat de benodigde CPU-tijd geen enkel obstakel
vormt voor het oplossen van een probleem met realistische omvang; dit is indien een efficient
algoritme gebruikt wordt. De voorwaarde is evenwel dat er gebruik gemaakt wordt van een com-
puternetwerk met voldoende intern geheugen. Zo niet, maakt een te grote toestandsruimte het
model onoplosbaar omwille van de omvangrijke matrices. Dit kan bijvoorbeeld verholpen worden
door het aantal mogelijke prijsniveaus te verlagen of door een aantal goederen te combineren in
’batches’.
Verder onderzoek
Dankzij de realiteitszin die aanwezig is in dit model kunnen een aantal nuttige inzichten beko-
men worden. Desalniettemin dient er rekening gehouden te worden met een aantal beperkingen
van dit onderzoek. Er worden immers nog steeds een aantal vereenvoudigende veronderstellingen
gemaakt die het model minder complex maken maar tevens de praktische toepasbaarheid ver-
minderen. Zo worden er belangrijke beperkende veronderstellingen gemaakt in verband met de
kansverdelingen van zowel de vraag als het prijsniveau. Het aantal mogelijke scenario’s wat be-
treft het prijsniveau is bijgevolg relatief beperkt in dit model. Het kan bijvoorbeeld interessant
zijn om het model zodanig aan te passen, dat de invloed op het bestelbeleid kan geanalyseerd wor-
den van een lange trage prijsstijging gevolgd door een korte grote prijsdaling of vice versa. Ook
de kansverdeling van de levertermijn zal vaak niet overeenkomen met de werkelijkheid. Deze
onzekere levertermijn wordt immers volledig bepaald door een enkele parameter die zowel de ge-
middelde levertermijn als de variabiliteit hiervan vastlegt. Dit zou kunnen verholpen worden door
het invoeren van nog een extra dimensie in de Markov-keten maar dit zou het model nagenoeg
82

onoplosbaar maken. Het kan echter de moeite lonen hier nog verder onderzoek naar te verrichten.
Om de realiteit beter te benaderen, zou het ten slotte ook interessant zijn de impact op het bestel-
beleid te analyseren van hoeveelheidskortingen en tijdelijke prijskortingen, alsook de impact van
niet-lineaire voorraadkosten.
Het is mogelijk om verder te bouwen op het model uit deze masterproef door enkele van deze ver-
onderstellingen te laten vallen. Anderzijds kan het model ook aangepast worden aan de specifieke
situatie van een welbepaald bedrijf door middel van het aanpassen van deze veronderstellingen.
Een aantal belangrijke veronderstellingen zijn echter onlosmakelijk verbonden aan de gebruikte
methodiek. Zo zorgt het gebruik van een stationaire Markov-keten er voor dat de relevante para-
meters zoals de vraag, de kosten en de prijsevoluties steeds constant blijven in de tijd. Dit heeft
enkele belangrijke implicaties, zoals de onmogelijkheid om seizoensfluctuaties op te nemen in dit
model wat betreft de vraag. Alsook beperkt dit de toepasbaarheid van het model tot goederen in
een stabiele levensfase. Een laatste belangrijke beperking van het besproken model is dat enkel de
kostenzijde wordt bekeken en de inkomstenzijde ten gevolge van de doorverkoop van de goederen
wordt genegeerd. Vaak wordt de verkoopprijs immers aangepast aan de inkoopprijs en heeft deze
verkoopprijs vervolgens een invloed op de grootte van de vraag.
Hoewel het model specifiek gebouwd is voor goederen die aangekocht worden zou het ten slotte
relatief eenvoudig kunnen worden aangepast en toegepast in een productie-omgeving. De stochas-
tische vraag wordt in deze situatie vervangen door een eindige productiesnelheid. Hierbij moet
dan rekening gehouden worden met vaste instelkosten voor het afstemmen van de machines in
plaats van vaste bestelkosten. Bovendien moet in deze situatie ook rekening gehouden worden
met eventuele schaalvoordelen, vergelijkbaar met hoeveelheidskortingen in het model uit deze
masterproef.
83

Bibliografie
[1] Richard Bellman. A markovian decision process. Journal Of Mathematics And Mechanics,
6(4):679–684, 1957.
[2] S. Chopra and P. Meindl. Supply Chain Management. Strategy, planning & operation. Pear-
son Education, New Jersey, 4 edition, 2010.
[3] J.L. Doob. Stochastic processes. John Wiley and Sons, 1953.
[4] Paul Durlinger. Wat kost voorraad? IT logistiek, (3):16–17, maart 2005.
[5] K. Fogel and M. Bar. Open Source Development With CVS. Paraglyph Press, 3 edition, 2003.
[6] Ford W. Harris. How many parts to make at once. The Magazine of Management, 10(2):135–
136, 1913.
[7] M. Helmreich. Best Practices of Adopting Open Source Software in Closed Source Software
Products. PhD thesis, Diplomarbeit, Friedrich-Alexander University of Erlangen-Nurnberg,
2011.
[8] F. S. Hillier and G.J. Lieberman. Introduction to Operations Research. McGraw-Hill, Sin-
gapore, 3 edition, 2010.
[9] W. Hopp and M. Spearman. Factory Physics, chapter Inventory Control: From EOQ to RDP.
McGraw-Hill, 3 edition, 2008.
[10] R.A. Howard. Dynamic Programming and Markov Processes. The M.I.T. Press, 1960.
[11] REM Associates of Princeton Inc. Consultants to Business Management. Methodology of
calculating inventory carrying costs, Augustus 2012. URL: http://www.remassoc.
com/portals/0/remprecc.pdf.
[12] Yan K. and Kulkarni V. Optimal inventory policies under stochastic production and demand
rates. Stochastic Models, 24(2):173–190, 2008.
i

[13] S. Manigart and M. Meuleman. Financing entrepreneurial companies. Larcier, Gent, Bel-
gium, 2004.
[14] G. Miller. Aggregate inventory management. PROACTION, 2006.
[15] M.L. Puterman and M.C. Shin. Modified policy iteration algorithms for discounted markov
decision problems. Management Science, 24, 1978.
[16] H. Richardson. Control your costs then cut them. Transportation and Distribution,
36(12):94, December 1995.
[17] D.C. Schmidt and A. Porter. Leveraging open-source communities to improve the quality &
performance of open-source software. In Proceedings of the 1st Workshop on Open Source
Software Engineering, 2001.
[18] Nigel Slack, Stuart Chambers, and Alan Johnston. Operations and Process Management:
Principles and Practice for Strategic Impact. Financial Times Prentice Hall, Harlow, UK, 2
edition, 2008.
[19] J.R. Stock and D.M. Lambert. Strategic Logistics Management. Irwin Professional Publish-
ing, 2 edition, 1987.
[20] Richard S Sutton. On the significance of markov decision processes. Environment,
(1327):273–282, 1997.
[21] R.S. Sutton and A.G. Barto. Reinforcement learning: An introduction. Neural Networks,
IEEE Transactions on, 9(5):1054–1054, 1998.
[22] Jinn-Tsair Teng, Maw-Sheng Chern, and Ya-Lan Chan. Deterministic inventory lot-size
models with shortages for fluctuating demand and unit purchase cost. International Trans-
actions in Operational Research, 12(1):83–100, 2005.
[23] H. C. Tijms. Stochastic Modelling and Analysis: A Computational Approach, chapter Marko-
vian Decision Processes and their Applications, pages 159–255. John Wiley & Sons Inc.,
New York, 1986.
ii

Appendix A
Lijst van de gebruikte symbolen
Voorraadbeheer
Q Bestelhoeveelheid
D Jaarlijkse vraag
P Inkoopprijs van het product
C0 Bestelkost per bestelling
Ch = h · P Voorraadkost per eenheid per tijdseenheid
h Voorraadkost als een percentage van de prijs
EOQ = Q∗ Economic Order Quantity = Optimale bestelhoeveelheid
L Levertermijn
Markov-ketens en Markoviaanse beslissingsprocessen
Si Verzameling van mogelijke toestanden
Pr Kans
pij Een-staps overgangskans van toestand i naar toestand j
P (n) n-staps transitiematrix
πi Steady-state kans voor toestand i
di = ai Actie die gekozen wordt in toestand i
Cik De kost indien actie k ondernomen wordt in toestand i
φi Bestelbeleid in toestand i
iii

Φ Bestelbeleid
V (s) Waarde van de toestand s
γ Disconteringsfactor
Pa(s, s′) Transitiematrix indien actie a gekozen wordt
Ra(s, s′) Kostmatrix indien actie a gekozen wordt
Model 1: Inleidend model met een beperkte toestandsruimte
p De kans op vraag op tijdstip t
α De kans op een prijsdaling op tijdstip t
β De kans op een prijsstijging op tijdstip t
p De kans dat er geen vraag is op tijdstip t
α De kans dat de prijs niet daalt
β De kans dat de prijs niet stijgt
C0 Bestelkost
Ch Voorraadkost
PL Laag prijsniveau
PH Hoog prijsniveau
d Disconteringsfactor
St De toestand (voorraad, prijs) op tijdstip t
pij Pr{St+1 = j|St = i}
⊗ Kronecker product
Model 2: Model met een uitgebreide toestandsruimte
Pi Prijsniveau i
P Verzameling van mogelijke prijsniveaus
K Aantal mogelijke prijsniveaus
C Maximale voorraadniveau
v Factor gebruikt bij het modelleren van de prijsfluctuaties
iv

Model 3: Model met een onzekere levertermijn
CV Kost van verloren vraag
κ Kans op levering
κ 1− kans op levering
L Levertermijn
v

















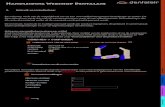


![Productie en Voorraadbeheer 1: - Forecastingdurlinger.nl/files/boeken/Forecasting-2014.pdf · MRP-filosofie (Orlicky [1974]) is de onafhankelijke klantenvraag de input ... en Romeinen](https://static.fdocuments.nl/doc/165x107/5bb3926409d3f2d3728ba5c8/productie-en-voorraadbeheer-1-mrp-filosofie-orlicky-1974-is-de-onafhankelijke.jpg)