Oplossingen WAI

Bert De Deckere

-1

-0.5

0

0.5

1

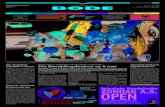
-1 -0.5 0 0.5 1

Pn(x)

x

P0

P1

P2

P3

P4

Inhoudsopgave

1 Afleidbaarheid 31.1 Legendreveelterm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31.2 Kettinglijn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51.3 Limieten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

2 Lineaire differentiaalvergelijkingen 62.1 Voorwaarden LDV met constante coefficienten . . . . . . . . . . . . . . . . . 62.2 LDV herleiden tot LDV met constante coefficienten . . . . . . . . . . . . . . 72.3 Basisoplossingen LDV . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82.4 Zoutvat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92.5 Unieke oplossing . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102.6 Radioactief verval . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112.7 Wronskiaan . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12

3 Niet-lineaire differentiaalvergelijkingen 133.1 Verticaal cilindrisch vat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 133.2 Orthogonale baan aan de cissoıde . . . . . . . . . . . . . . . . . . . . . . . . 14

4 Oneigenlijke integralen 154.1 Fourierbeeld . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 154.2 Gedrag Fourierbeeld . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 174.3 Convergentieonderzoek . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 184.4 Onderzoek laplacetransformeerbaarheid . . . . . . . . . . . . . . . . . . . . 194.5 Oneigenlijke integraal uitrekenen . . . . . . . . . . . . . . . . . . . . . . . . 204.6 Duplicatieformule van Legendre . . . . . . . . . . . . . . . . . . . . . . . . . 21

5 Functiereeksen 225.1 d’Alembert en Cauchy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 225.2 Convergentieonderzoek . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 235.3 Reekssomfunctie + convergentie bepalen . . . . . . . . . . . . . . . . . . . . 245.4 Reekssom bepalen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 265.5 Z-transformatie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 275.6 Fourierreeks + Parseval . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 295.7 Eigenschap Fourierreeksen . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31

6 Bewijzen 326.1 Regel van Leibniz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 326.2 Uniek Z-beeld . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 336.3 Integraaltest reeksen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 346.4 Tweede afgeleide . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36

1

Voorwoord

De opgaven die in deze bundel verwerkt zijn, zijn oefeningen die bij de moeilijkere horen.Deze kunnen afkomstig zijn van oude examens, de extra opgaven, ...Indien je fouten mocht aantreffen gelieve dit dan te melden via bert.dedeckere@ugent.be

2

1 Afleidbaarheid

1.1 Legendreveelterm

• De legendreveelterm van de n-de graad wordt gedefinieerd door:

Pn(x) =1

2n · n!· d

n

dxn(x2 − 1)n

Toon aan dat Pn, n verschillende nulpunten heeft in het interval ]− 1, 1[.(De eerste 5 Legendre polynomen zijn afgedrukt op de titelpagina.)

BewijsBeschouw (x2 − 1)n, deze veelterm heeft een nulpunt voor x = ±1, overeenkomstigde stelling van Rolle is er dus een punt c ∈]− 1, 1[ waarvoor geldt ((x2 − 1)n)′ = 0.Nogmaals deze stelling toepassen levert een punt d1 ∈]− 1, c[ en d2 ∈]c, 1[, waarvoorgeldt ((x2 − 1)n)′′ = 0.Doordat P1 = x, 1 nulpunt heeft kan door het inductieprincipe besloten worden datPn, n verschillende wortels heeft in het interval ]− 1, 1[.

• Toon aan dat Pn(1) = 1 en Pn(−1) = (−1)n.

Pn =1

2n · n!· d

n

dxn(x2 − 1)n

=1

2n · n!· d

n

dxn(x+ 1)n(x− 1)n

=1

2n · n!·n∑k=0

(n

k

)((x+ 1)n)(k) · ((x− 1)n)(n−k)

=1

2n · n!·

(n! · (x+ 1)n +

n∑k=1

(n

k

)((x+ 1)n)(k) · ((x− 1)n)(n−k)

)Waaruit volgt dat Pn(1) = 1. Op een analoge manier kan het volgende bekomenworden (dit volgt ook uit de symmetrie van de regel van Leibniz):

Pn =1

2n · n!·

(n! · (x− 1)n +

n∑k=1

(n

k

)((x− 1)n)(k) · ((x+ 1)n)(n−k)

)Waaruit volgt dat Pn(−1) = (−1)n.

3

• Toon aan dat (x2 − 1)P ′′n + 2xP ′n − n(n+ 1)Pn = 0.

Beschouw onderstaande gelijkheid:

(x2 − 1) · d(x2 − 1)n

dx= 2nx(x2 − 1)n

Dit n+ 1 keer afleiden met de regel van Leibniz levert:

n+1∑k=0

(n+ 1

k

)(x2−1)(k) ·

((x2 − 1)n

)(n−k+2)= 2n

n+1∑k=0

(n+ 1

k

)x(k) ·

((x2 − 1)n

)(n−k+1)

Het linkerlid uitwerken levert:

(x2 − 1) ·((x2 − 1)n

)(n+2)+ (n+ 1)2x

((x2 − 1)n

)(n+1)+ n · (n+ 1)

((x2 − 1)n

)(n)Idem voor het rechterlid:

2nx((x2 − 1)n

)(n+1)+ 2n(n+ 1)

((x2 − 1)n

)(n)En uiteindelijk beide terug combineren:

(x2 − 1)P ′′n + 2xP ′n − n(n+ 1)Pn = 0

4

1.2 Kettinglijn

Een kettinglijn is in de omgeving van de oorsprong te benaderen door een parabool. Gana tot in welke orde beide inderdaad samenvallen.

Eerst en vooral is het belangrijk om op te merken dat de kettinglijn gegeven wordt doorcosh(x). Als je tussen je 2 vingers een touw neemt, dan zal dit touw het voorschrift vande kettinglijn volgen. De eerste 3 termen van het Taylorpolynoom van cosh(x) wordengegeven door:

cosh(x) ≈ 1 +x2

2!+x4

3!+ . . .

En bijgevolg valt de kettinglijn tot de derde orde samen met een parabool (de derde ordeterm is 0).

1.3 Limieten

Onderstel dat de functie f afleidbaar is in ]a,+∞[ en dat

limx→∞

(f(x) + f ′(x)) = A

Dan geldt limx→∞

f(x) = A en limx→∞

f ′(x) = 0.

BewijsEerst en vooral kan dit ook grafisch worden ingezien. Als f(x) een horizontale asymptootvertoont, dan is zijn richtingscoefficient = 0 en dus is ook f ′(x) = 0.Om dit formeel te bewijzen maken we gebruik van de omgekeerde stelling van l’hopital:

limx→∞

(f(x) + f ′(x)) = limx→∞

ex · f(x) + ex · f ′(x)

ex

= limx→∞

f(x) · ex

ex

= limx→∞

f(x) = A

5

2 Lineaire differentiaalvergelijkingen

2.1 Voorwaarden LDV met constante coefficienten

Stel een nodige en voldoende voorwaarde voor de functies p en q op, opdat de LDV

y′′ + p(x)y′ + q(x)y = 0

zou kunnen worden herleid d.m.v. een verandering van onafhankelijke variabele, tot eenLDV met constante coefficienten.

Je weet dat je de DV van Euler kan herleiden tot een met constante coefficienten, pro-beer dit wat uit te buiten.

C1x2y′′ + C2xy

′ + C3y′ = 0

Nu nog wat aanpassen:

y′′ +y′

C ′1x+

y′

C ′2x2

= 0

Als je dus p(x) kunt schrijven als 1/(C1 · x) en q(x) als 1/(C2 · x2), dan kan je hemherleiden tot een DV met constante coefficienten. Dit is tegelijk een nodige en voldoendevoorwaarde.Dat het ook een nodige voorwaarde is kan als volgt worden ingezien: stel dat je hemkan schrijven als een DV met constante coefficienten dan kan je ook terugkeren naar deoorspronkelijke DV door de inverse substitutie toe te passen. Op die manier keer je terugnaar de Euler-DV en vormt het een nodige en voldoende voorwaarde.Dit gebeurt onder de aanname dat de omzetting naar een DV met constante coefficientenuniek is, en dat is hij ook anders zou je verschillende oplossingen bekomen (op een constantefactor na).

6

2.2 LDV herleiden tot LDV met constante coefficienten

Toon aan dat elke oplossing van de LDV

xy′′ − 2y′ + xy = 0

tevens oplossing is van een differentiaalvergelijking van de vierde orde met constantecoefficienten.Los deze laatste op en leid hieruit de algemene oplossing van de gegeven LDV af.

Indien we linker- en rechterlid tweemaal afleiden bekomen we:

(xy′′ − 2y′ + xy)′′ = 0

(y′′ + xy′′′ − 2y′′ + y + xy′)′ = 0

(xy′′′′ + y′ + xy′′ + y′) = 0

Voor nu de substitutie 2y′ = xy′′ + xy uit:

xy′′′′ + 2xy′′ + xy = 0

y′′′′ + 2y′′ + y = 0

De oplossing van deze LDV luidt:

y(x) = C1 cos(x) + C2x cos(x) + C3 sin(x) + C4x sin(x)

We verkrijgen dus een vierdimensionale oplossingenruimte, terwijl er maar 2 gewenst zijn.Indien we deze oplossing echter terug substitueren in de oorspronkelijke DV, dan verkrijgenwe:

2 sin(x)(C1 − C4)− 2 cos(x)(C2 + C3) = 0

Waaruit direct de voorwaarden voor 2 lineair onafhankelijke oplossingen kunnen wordenafgelezen, nl.

C1 = C4

C2 = −C3

En dus luidt de oplossing:

y(x) = C ′1(x cos(x)− sin(x)) + C ′2(cos(x) + x sin(x))

7

2.3 Basisoplossingen LDV

Toon aan dat voor elke N ∈ N de LDV

xy′′ − (x+N)y′ +Ny = 0

een exponentiele en een veeltermfunctie als basisoplossingen bezit.

Uit het gevraagde volgt dat er een exponentiele als basisoplossing is. Als je y1(x) = ex

substitueert in de LDV, zie je inderdaad dat dit een oplossing is. Je hebt nu al 1 oplossing.De andere kan je vinden door te werken met de wronskiaan:

W ′(x) = −p(x)W (x)

=x+N

xW (x)

Deze DV oplossen geeft:W (x) = ex · xN = y′1y2 − y′2y1

y1 weet je al, dus de ex mag je schrappen. Daarna kan je met Lagrange de tweede oplossingvinden, namelijk:

y2 = ex ·∫xN

ex

Dit invoeren in Maple gaat als volgt:

assume(N::natural):

simplify(exp(x)*int(x^N/exp(x), x));

Waaruit de oplossing voor y2 volgt:

y2 = −N ! ·N∑k=0

xk

k!

8

2.4 Zoutvat

Een vat met een capaciteit van 100 l is volledig gevuld met water waarin 10 kg zout isopgelost. Per minuut wordt 5 l zuiver water aan het vat toegevoegd. Wat overloopt, navolledige menging, wordt in een ander vat met dezelfde capaciteit geleid, dat oorspronke-lijk volledig met zuiver water was gevuld. De vloeistof in het tweede vat wordt eveneensvolledig gemengd. Wanneer zal de hoeveelheid zout in het tweede vat maximaal zijn?

De concentratie Q in het eerste vat wordt gegeven door onderstaande DV:

dQ(t)

dt= −Q(t) · 5

100

Bovenstaande oplossen met de beginvoorwaarde Q(0) = 110 , levert:

Q(t) =e−

t20

10

Dat komt terecht in het vat eronder. Dus de hoeveelheid zout Z in het tweede vat wordtgegeven door:

dZ(t)

dt= Q(t) · 5− Z(t) · 5

100

Dit oplossen met de beginvoorwaarde Z(0) = 0 geeft je:

Z(t) =t · e−

t20

2

Nu nog het maximum zoeken, dus afleiden en nulpunten zoeken geeft je de extrema opt = 0 en 20.

9

2.5 Unieke oplossing

In welk gebied bezit het beginvoorwaardenprobleemy′′ + y = h(x)y(0) = 0y′(0) = 1

Waarbij

h(x) =

{x x ≤ ππ · eπ−x x > π

een oplossing die er tweemaal continu differentieerbaar is?Bepaal deze oplossing.

Met behulp van Maple kan voor ieder deelinterval de oplossing bepaald worden. Hier-bij dienen de beginvoorwaarden opgelegd te worden aan de functie die daar gedefinieerdis. Dit geeft:

• x ≤ π y′′1 + y1 = h(x)y(0) = 0 → y1(x) = xy′(0) = 1

• x > π

y′′2 + y2 = π · eπ−x → y2(x) = C1 · sin(x) + C2 · cos(x) +π · eπ−x

2

Er werd gevraagd naar een oplossing die tweemaal continu differentieerbaar is, dus moeteny1 en y2 ’aansluiten’. Dit houdt in dat de waarde van y1 en y2 en hun afgeleiden in hetpunt x = π gelijk moeten zijn aan elkaar, of dus:{

y1(π−) = y2(π+)y′1(π−) = y′2(π+)

Dit oplossen levert C1 = −1 − π2 en C2 = −π

2 . Indien we beide functies daarna tweemaalafleiden dan zien we dat ook hun tweede afgeleide in x = π gelijk is aan elkaar, dus deoplossing is tweemaal continu afleidbaar in gans R.

10

2.6 Radioactief verval

Een radioactief isotoop vervalt derwijze op elk moment de hoeveelheid materiaal die pertijdseenheid desintegreert recht evenredig is met de beschikbare hoeveelheid op dit moment.Men constateert dat van 100 mg radioactief thorium 234 na een week nog 82, 04 mg rest.

• Bepaal de halfwaardentijd van thorium 234, dit is de tijdspanne waarin de helft vande hoeveelheid radioactief materiaal is gedesintegreerd (en dus de helft overblijft).

Stel H(t) gelijk aan de hoeveelheid radioactief materiaal en noem k de evenredig-heidsconstante, dan geldt:

dH(t)

dt= −k ·H(t)

Deze differentiaalvergelijking oplossen met Maple geeft H(t):

H(t) = 100 · e−kt

Na 7 dagen is er nog 82, 04 mg over, dus k = 0, 028.Hierna bepalen wanneer er nog 50 mg overblijft levert t = 24, 5 dagen.

• Als men initieel (t = 0) beschikt over 100 mg thorium 234 en dagelijks 1 mg eraantoevoegt, bepaal dan de hoeveelheid radioactief materiaal na een week.

Hiervoor zetten we Maple aan het werk:

for i from 1 to 7 do

G:=t->100*exp(-0.02828046468*t):

m:=G(i) + 1;

print(’na’, i, ’dagen’, ’is’, ’er’, m, ’g’, ’radioactief’, ’materiaal’);

unassign(‘G‘);

dsolve({diff(G(t), t) = -k*G(t), G(0)=m}, G(t));

end do:

Dit levert na 7 dagen 83, 04 mg thorium op.

11

2.7 Wronskiaan

De Wronskiaanse determinant van twee oplossingen van de differentiaalvergelijkingy′′ − 3x2y′ + y = 0 kan worden geschreven onder de vorm Cex

3.

Er geldt:

W ′(x) = −p(x) ·W (x)

W ′(x)

W (x)= 3x2

ln(W (x)) = x3 + C

W (x) = C · ex3

Analoog als W (x) < 0, dus waar.

12

3 Niet-lineaire differentiaalvergelijkingen

3.1 Verticaal cilindrisch vat

In de bodem van een verticaal cilindrisch vat, met oppervlakte grondvlak S cm2 is eenschijfvormige opening van q cm2 aangebracht die kan worden gesloten d.m.v. een dia-fragma. Het vat wordt tot op een hoogte h0 gevuld, waarna het diafragma geopend wordtop het tijdstip t = 0. De oppervlakte van de opening is recht evenredig met de tijd t enbereikt de maximale waarde q op het tijdstip t = T . Welke is de hoogte van de vloei-stofkolom op dat tijdstip T? De snelheid van de vloeistof wordt gegeven door de wet vanTorricelli: v =

√2gh, h zijnde de hoogte van de vloeistofkolom.

De bedoeling is eerst om een functievoorschrift op te stellen voor het volume. De ver-andering van het volume (dVdt ), is gelijk aan het debiet dat binnenkomt - het debiet datterug weggaat. Symbolisch geeft dit:

dV (t)

dt= D(t)in −D(t)uit

Er komt niks binnen, dus die eerste term valt weg. Het debiet dat naar buiten stroomt isgelijk aan het product van de snelheid met de grootte van de opening. Zie het voor je alseen buis waarvan de lengte toeneemt met de tijd. Het volume van de buis is je debiet enis dus gelijk aan het product van snelheid en opening:

D(t)uit = q(t) · v(t)

De grootte van dit gat is op t = 0,= 0 en op t = T,= q. Je hebt dus 2 punten waardoorje een rechte kan tekenen. Het voorschrift van deze rechte = q(t) en is dus:

q(t) =qt

T

De snelheid wordt gegeven door Torricelli, maar hier zit je met een onbekende h. Je weetechter dat V (t) = S · h, dus alles samen geeft dit:

dV (t)

dt= −D(t)uit = −qt

T·√

2gV (t)

S

Nu nog de beginvoorwaarden, nl. V (0) = S ·h0. Dit invoeren in Maple geeft je als oplossing:

V (T ) = S

(√h0 −

qT√g

S√

8

)2

De hoogte = VS en is dus:

h(T ) =

(√h0 −

qT√g

S√

8

)2

13

3.2 Orthogonale baan aan de cissoıde

Bepaal de orthogonale banen aan de schaar cissoıden gegeven door (2a− x) · y2 = x3.

Merk vooreerst op dat als 2 rechten elkaar loodrecht snijden, dat het product van hunrichtingscoefficienten gelijk is aan -1. De richtingscoefficient van de orthogonale krommewordt dus gegeven door − 1

y′(x) . De afgeleide van een cissoıde ziet er als volgt uit (Maple):

−y(x)2 + (2 · (2a− x)) · y(x) · dy(x)

dx= 3 · x2

We kunnen hierin de 2a− x vervangen door x3

y(x)2(zie opgave), dit levert:

−y(x)2 +

(2x3

y(x)

)· dy(x)

dx= 3 · x2

Door nu de eerdervermelde substitutie toe te passen − 1y′(x) wordt x in functie van y ge-

plaatst. Uiteindelijk levert dit de volgende DV die dient opgelost te worden:

−y2 −(

2x(y)3

y

)· dx(y)

dy= 3 · x(y)2

De oplossing hiervan luidt:

x2 =−a2 · y2 + 1 +

√a2 · y2 + 1

a2

-2

-1.5

-1

-0.5

0

0.5

1

1.5

2

-2 -1.5 -1 -0.5 0 0.5 1 1.5 2

14

4 Oneigenlijke integralen

4.1 Fourierbeeld

Bepaal het Fourierbeeld G(ω) van de functie g(t) = 1(1+t2)2

, t ∈ R

Om deze oefening op te lossen maken we gebruik van Fourierparen.

g(t) =1

1 + t2→ F{g(t)} = π · e−|ω|

F{g′(t)} = iωF{g(t)}

F{−2t

(1 + t2)2

}(ω) = iωπe−|ω|

Nu nog wat spelen met de constanten:

F{−it

(1 + t2)2

}(ω) = −ωπe

−|ω|

2

Er geldt:d

dωF{f(t)}(ω) = F{−itf(t)}(ω)

Stel nu:

f(t) =1

(1 + t2)2

Verder uitwerken:

F{f(t)}(ω) =

∫−ωπe

−|ω|

2dω

En dus:F{f(t)}(ω) =

π

2· (1 + |ω|)e−|ω| + C

F{f(t)}(0) =

∞∫−∞

f(t)dt

Dit is gelijk aan π2 (Maple). Dus is ook C = 0. Dit geeft het uiteindelijke antwoord:

F{f(t)}(ω) =π

2· (1 + |ω|)e−|ω|

15

Een andere mogelijkheid om deze oefening op te lossen is via zogenaamde convolutie. Eris een stelling die het volgende zegt: F(f(t) · g(t))(ω) = F(f(t))(ω) ∗ F(g(t))(ω), waar-bij ∗ staat voor het convolutieproduct. Dit product is gedefinieerd als (voor de Fourier-

transformatie): (f ∗ g)(x) =∞∫−∞

f(u)g(x− u)du

Met deze kennis is het mogelijk om op een relatief eenvoudige manier het Fourierbeeld teberekenen.

F(

1

(1 + t2)2

)= F

(1

1 + t2

)∗ F

(1

1 + t2

)

=π

2e−|ω| ∗ π

2e−|ω|

=π

2

∞∫−∞

e−|t|e−|ω−t|dt

Nu een gevalsondersheid maken tussen ω <, = en > 0 geeft:

G(ω) =

π2 (1 + ω)e−ω : ω > 0π2 : ω = 0π2 (1− ω)eω : ω < 0

En dit is net hetzelfde als wat we eerder bekwamen.

16

4.2 Gedrag Fourierbeeld

• als f(t) reeelwaardig en even is, dan is F(ω) reeelwaardig en even

Als f(t) reeelwaardig en even is, kan het fourierbeeld als volgt geschreven worden:

F(ω) =

∞∫−∞

f(t)e−iωt

= 2

+∞∫0

f(t) · cos(ωt)dt

Wat terug reeelwaardig is. Om nu het (on)even karakter te onderzoeken kijken wenaar het gedrag onder ω. Dankzij de cosinus is F(−ω) = F(ω), dus F(ω) is even.

• als f(t) zuiver imaginair en oneven is, dan is F(ω) zuiver imaginair en oneven.

Als f(t) reeelwaardig en even is, kan het fourierbeeld als volgt geschreven worden:

F(ω) =

∞∫−∞

f(t)e−iωt

= −2i

+∞∫0

f(t) · sin(ωt)dt

f(t) was al imaginair, dus krijgen we een reeelwaardige functie terug, die oneven isdankzij de sinus. De stelling was dus vals.

17

4.3 Convergentieonderzoek

Is onderstaande integraal convergent of divergent:

∞∫0

ln(x)

x2 − 1dx

Bij deze integraal is er een probleem voor x = 0, 1,∞, dus splitsen we de integraal als volgtop:

∞∫0

ln(x)

x2 − 1dx =

12∫

0

ln(x)

x2 − 1dx+

1∫12

ln(x)

x2 − 1dx+

2∫1

ln(x)

x2 − 1dx+

∞∫2

ln(x)

x2 − 1dx

Het convergentieonderzoek voor de eerste integraal verloopt via onderstaande limiet:

limx→0

xα ln(x)

x2 − 1

Kies hierbij α = 12 en pas daarna l’hopital toe:

limx→0

ln(x)x2−1x12

H= lim

x→0

1x

2x32− 1

2x32+ 1

2x−12

x

= limx→0

2√x

3x2 + 1= 0

K = 0 en α < 1, dus convergent.De volgende integraal heeft een probleem in de bovengrens 1, gewoon de limiet uitrekenengeeft echter:

limx→1

ln(x)

x2 − 1

H= lim

x→1

1x

2x=

1

2

Dus ook deze integraal is convergent.Nu nog de laatste, deze heeft ook een probleem in de bovengrens, de convergentietest geeft:

limx→+∞

xα ln(x)

x2 − 1

Kies ditmaal alpha = 3/2 en pas daarna opnieuw l’hopital toe:

limx→+∞

ln(x)x2−1x32

H= lim

x→+∞

1x

2x52−(x2−1) 3

2x12

x3

= limx→+∞

2x32

x2 + 3= 0

α > 1 en K ≥ 0, dus ook dit is in orde. De volledige integraal convergeert dus.

18

4.4 Onderzoek laplacetransformeerbaarheid

Gegeven is de functie g die aan de volgende voorwaarden voldoet:

• g is causaal

• g is begrensd in [0,+∞[

• g is continu in [0, a] en in [a,+∞[ en vertoont in a een sprongpunt

• g′ is continu in [0, a] en in [a,+∞[

• g is laplacetransformeerbaar in Re z > 0 met laplacebeeld L(z)

Onderzoek de laplacetransformeerbaarheid van g′ en stel desgevallend een formule op diehet laplacebeeld van g′ uitdrukt in functie van L(z).

Met behulp van de definitie voor de laplacetransformatie bekom je:

L{g′(t)

}(z) =

∞∫0

g′(t)e−ztdt

=

b∫0

g′(t)e−ztdt+

∞∫b

g′(t)e−ztdt

=[g(t)e−zt

]b−0

+ z

b∫0

g(t)e−ztdt+[g(t)e−zt

]∞b+

+ z

∞∫b

g(t)e−ztdt

= zL{g(t)}+ (g(b−)− g(b+)) · e−zb

Je weet dat g(t) causaal is, dus de linkerlimiet in 0 = 0. Je weet ook dat hij continu is in[0, a], dus g(0) = 0.

19

4.5 Oneigenlijke integraal uitrekenen

Bepaal de waarde van∞∫0

eix√xdx. Werkwijze:

Γ

(1

2

)=√π =

∞∫0

e−xx−12 dx

= −1

i

∞∫0

eix√−ix

dx

=i2

i52

∞∫0

eix√x

dx

= (−1)−14

∞∫0

eix√x

dx

(−1)14 ·√π =

∞∫0

eix√x

dx

Op een analoge manier kan dezelfde integraal met cosinus of sinus worden berekend, doorde cosinus of sinus uit te schrijven m.b.v. e-machten.

20

4.6 Duplicatieformule van Legendre

Bewijs de duplicatieformule van Legendre: 22p−1Γ(p)Γ(p+ 1

2

)=√πΓ(2p)

• Stel m = n = 12 , dan krijg je:

Γ(12

)22Γ(1)

=

π2∫

0

sin0(t) cos0(t)dt

Γ(12

)22

=π

2

Γ

(1

2

)=√π

• Het volgende gedeelte in het bewijs gaat als volgt:

Γ(p)Γ(p)

2Γ(2p)=

π2∫

0

sin2p−1(t) cos2p−1(t)dt

=1

22p−1

π2∫

0

sin(2t)2p−1dt

= 2−2pπ∫

0

sin(u)2p−1du

= 2−2p+1

π2∫

0

sin(u)2p−1du

= 2−2pΓ(p)Γ

(12

)Γ(p+ 1

2

)Beide zaken samenbrengen levert de duplicatieformule:

22p−1Γ(p)Γ

(p+

1

2

)=√πΓ(2p)

21

5 Functiereeksen

5.1 d’Alembert en Cauchy

Hieronder zal aangetoond worden dat de test van d’Alembert steeds hetzelfde resultaatgeeft als de test van Cauchy.

limn→∞

∣∣∣∣an+1

an

∣∣∣∣ = limn→∞

n√|an|

limn→∞

|an+1|n = limn→∞

|an|n+1

Dankzij deze gelijkheid is het mogelijk om bijvoorbeeld onderstaande limiet op een een-voudige manier uit te rekenen:

limn→∞

n√n!

Hierin kan de Cauchy-test voor de reeks n! herkend worden. Door de analoge test vand’Alembert uit te voeren (die hetzelfde resultaat geeft) bekom je:

limn→∞

n√n! = lim

n→∞

(n+ 1)!

n!

= +∞

22

5.2 Convergentieonderzoek

Onderzoek de puntsgewijze, de absoluut puntsgewijze en de gelijkmatige convergentie vande reeks:

∞∑k=0

(−1)k · x2k+1

2k + 1

De reekssomfunctie is gelijk aan arctan(x).

• Puntsgewijze convergentieDe puntsgewijze convergentie kan worden onderzocht met de stelling van Leibniz.De rij is dalend ⇔ x < 1, dus puntsgewijs convergent als x < 1. x ≥ 1 levert deharmonische reeks op, dus divergent.

• Absolute en uniforme convergentieVoor de absolute convergentie kunnen we gebruikmaken van d’Alembert:

limn→∞

∣∣∣∣an+1

an

∣∣∣∣ < 1

limn→∞

∣∣∣∣x2k+3

x2k+1

∣∣∣∣ < 1

|x| < 1

Uit de M-test volgt dat de reeks uniform convergent is op de compacta, dus uniformconvergent op [a, b]⇔ b > a ∧ a, b ∈]− 1, 1[

Voor de volgende reeks kan op een soortgelijke wijze tewerk worden gegaan:

x+

∞∑k=1

1 · 3 · ... · (2k − 1)x2k+1

2 · 4 · ... · 2k · (2k + 1)

Hierbij wordt de reekssomfunctie gegeven door arcsin(x).

23

5.3 Reekssomfunctie + convergentie bepalen

Gegeven:+∞∑n=1

(−1)n+1(n+ 1)xn−1

(n− 1)!

• Onderzoek de betrekkelijke, absolute en uniforme puntsgewijze convergentie van degegeven functiereeks voor x ∈ R.

Via de test van d’Alembert bekom je het convergentiegebied:

limn→+∞

∣∣∣∣ n!(n+ 1)

(n− 1)!(n+ 2)

∣∣∣∣ = +∞

Dus overal absoluut convergent en uniform convergent op de compacta, dus overaluniform convergent.

• Bepaal (door termsgewijze afleiding of primitivering) de reekssomfunctie.

Na 2 keer integreren verkrijg je:∫∫ +∞∑n=1

(−1)n+1(n+ 1)xn−1

(n− 1)!=

∫ +∞∑n=1

(−1)n+1(n+ 1)xn

n!

=

+∞∑n=1

(−1)n+1xn+1

n!

= −x · (e−x − 1)

Nu terug 2 keer afleiden:

+∞∑n=1

(−1)n+1(n+ 1)xn−1

(n− 1)!=

d2 (−x · (e−x − 1))

dx2

= 2 · e−x − x · e−x

24

• Toon aan dat+∞∑n=0

2n · (n+ 2)!

(n+ 1)! · n!

convergent is, en bepaal steunend op de vorige opgaven de reekssom.

Eerst proberen we hem in de vorm van de eerdere opgave te zetten door de sommatie-index aan te passen:

+∞∑n=0

2n · (n+ 2)!

(n+ 1)! · n!=

+∞∑n=0

2n · (n+ 2)

n!

=

+∞∑n=1

2n−1 · (n+ 1)

(n− 1)!

Stel nu x uit de eerdere vergelijking = −2 (ligt binnen je convergentiegebied) en danbekom je:

+∞∑n=0

2n · (n+ 2)!

(n+ 1)! · n!= 4 · e2

Hiermee is direct ook aangetoond dat de som convergent is.

25

5.4 Reekssom bepalen

Bepaal de reekssom van onderstaande som:

∞∑n=1

(−1)n · 22n · x2n

2n

Hiervoor gaan we als volgt te werk:

∞∑n=1

(−1)n · 22n · x2n

2n

ddx−−→

∞∑n=1

(−1)n · 22n · x2n−1

=1

x

∞∑n=1

(i2x)2n

=−4x

1 + 4x2

∫−→ −1

2ln(1 + 4x2)

Waarbij de integratieconstante = 0 (stel x = 0).

26

5.5 Z-transformatie

De n-de term van de numerieke rij (tn) (met n = 0, 1, 2, ...) is het rekenkundig gemiddeldevan zijn twee voorgangers.

• Bepaal het Z-beeld F van deze numerieke rij en het bijhorende convergentiegebied.

Z-transformatie nemen van beide leden:

Z(tn+2) = Z(tn+1 + tn

2

)Bovenstaande uitwerken geeft je:

Z(tn) =2t0z

2 + z(2t1 − t0)2z2 − z − 1

Waarbij |z| > max(1, 1/2).

• Bepaal een expliciete uitdrukking voor de term tn van de gegeven numerieke rij.

Oplossen met partieelbreuken:

Z(tn) =Az

2(z − 1)+

Bz

z + 12

Inverse Z-transformatie nemen:

tn = Z−1(

2t0 + 4t16

· z

z − 1+

2t0 − 2t13

· z

z + 12

)

=2t0 + 4t1

6+

2t0 − 2t13

·(−1

2

)n

• Onder welke voorwaarde is∞∑n=1

tn een convergente reeks? Bepaal in dit geval haar

reekssom

Het is een nodige voorwaarde dat de algemene term naar nul nadert. Dus de linkseterm moet = 0. De reekssom wordt dan gegeven door:

∞∑n=0

tn =∞∑n=0

2t0 − 2t13

·(−1

2

)n=

4t0 − 4t19

=4t19

En zodoende blijkt de nodige voorwaarde een voldoende.

27

• Onder welke voorwaarde(n) kan F geschreven worden als een negatieve machtreeksin termen van z? Bepaal deze negatieve machtreeks en haar convergentiegebied.

Een NMR start bij 1, terwijl dat bij de Z-transformatie niet het geval is. De be-doeling is dus om voorwaarden op te leggen zodat de NMR start bij 1. De eersteterm wordt gegeven door:

2t0 + 4t16

+2t0 − 2t1

3·(−1

2

)0

= 0

Dit verder uitwerken levert t0 = 0, wat dan ook de oplossing is.

• Stel t0 = 0. Bepaal een causaal laplace-origineel f van F en bepaal tevens het cor-responderende convergentiegebied.

Als we t0 = 0 nemen, dan kunnen we de inverse laplace transformatie berekenenmet behulp van de eerste vraag (en Maple):

L−1(

2t1z

2z2 − z − 1

)=

(t1e− t

2

3+

2t1et

3

)H(t)

En ook hier geldt Re(z) > 1

28

5.6 Fourierreeks + Parseval

Gegeven: f(t) = sinh(t), t ∈ [−1, 1].

• Ontwikkel de functie f in een fourierreeks met periode 2.

De functie is oneven, dus komen er enkel sinustermen voor. De coefficienten bkworden hierbij gegeven door:

bk =kπ(1− e2)(−1)ke−1

1 + k2π2

Dus het functievoorschrift is:

f(t) =∞∑n=1

kπ(1− e2)(−1)ke−1

1 + k2π2sin(kπt)

• Ontwikkel de functie g met g(t) = cosh(t) in een fourierreeks met periode 2 door defourierreeks van de functie f termsgewijs te integreren.

Na integratie blijven er enkel nog cosinustermen over. De coefficienten ak zijn hierbijgelijk aan:

ak =(e2 − 1)(−1)ke−1

1 + k2π2

En de integratieconstante wordt gegeven door de term a0, waarbij a0 = 2 sinh(1).Alles samen geeft dit het voorschrift voor de functie g(t):

g(t) = sinh(1) +

∞∑n=1

(e2 − 1)(−1)ke−1

1 + k2π2cos(kπt)

29

• Gebruik de gevonden fourierreeks(en) en de gelijkheid van Parseval om

∞∑n=1

1

(1 + k2π2)2

exact te berekenen.

De 3 verschillende termen uit de gelijkheid van Parseval hebben de volgende waarde:

1

2

1∫−1

f2(t)dt =sinh(1) cosh(1)

2+

1

2

a204

=(2 sinh(1))2

4= sinh(1)2

1

2

∞∑n=1

a2k =1

2

∞∑k=1

(e2 − 1)2e−2

(1 + k2π2)2

Deze 3 gelijkheden samen leveren:(sinh(1) · cosh(1)

2+

1

2− sinh(1)2

)· 2

(e2 − 1)2 · e−2=∞∑k=1

1

(1 + k2π2)2

30

5.7 Eigenschap Fourierreeksen

Zij f een functie die gedefinieerd is en stuksgewijze glad op het interval [−L,L] en daar-buiten periodiek wordt voortgezet.Als f oneven is en bovendien het punt

(L2 , 0)

als punt van symmetrie van haar grafiek be-

zit, dan is f ontwikkelbaar in een fourierreeks waarin enkel termen van de vorm sin(2kπxL

)optreden, k = 1, 2, ...

f is oneven, dus komen er enkel sinustermen in je fourierreeks voor. De sinuscoefficientenworden gegeven door:

bk =1

L·

L∫−L

f(x) · sin(kπx

L

)dx

Er is verder gegeven dat f(x) oneven is, dus kan je dat wat vereenvoudigen:

bk =2

L·L∫

0

f(x) · sin(kπx

L

)dx

Je weet dat bovenstaande integraal = 0 als

L/2∫0

f(x) · sin(kπx

L

)dx = −

L∫L/2

f(x) · sin(kπx

L

)dx

En dit is het geval als je integrandum oneven is t.o.v. de rechte x = L/2. Je weet al datf(x) oneven is tov L/2, dus is je integrandum oneven als de sinus een extremum bereiktvoor x = L/2. Dit is als:

kπx

L= Cπ +

π

2

Stel hierbij x = L/2, dan krijg je:k = 2C + 1

En aangezien C ∈ Z zal je integraal wegvallen als k oneven is. Dus blijven er enkel eventermen over.

31

6 Bewijzen

6.1 Regel van Leibniz

De vergelijking van Leibniz voor afgeleiden luidt:

(f · g)(k) =

k∑n=0

(k

n

)f (n) · g(k−n)

In wat volgt zal door inductie bovenstaande gelijkheid bewezen worden. Stel voor debasisstap k = 1, dan bekomen we:

(f · g)′ = f ′g + fg′

Dit is gelijk aan de productregel, dus de gelijkheid is correct voor k = 1. De inductiestapgaat dan als volgt:

(f · g)(k+1) =d

dx

k∑n=0

(k

n

)f (n) · g(k−n)

=

k∑n=0

(k

n

)d

dxf (n) · g(k−n)

=k∑

n=0

(k

n

)(f (k−n+1)g(n) + f (k−n)g(n+1)

)

=

(k∑

n=0

(k

n

)(f (k−n+1)g(n)

))+

(k+1∑n=1

(k

n− 1

)(f (k−n+1)g(n)

))

=

(k∑

n=1

(k + 1

n

)(f (k−n+1)g(n)

))+ f (k+1)g + fg(k + 1)

=

k+1∑n=0

(k + 1

n

)f (k−n+1)g(n)

32

6.2 Uniek Z-beeld

Veronderstel de rij an. Het Z-beeld van deze rij wordt gegeven door:

F (z) =

∞∑n=0

anzn

Veronderstel dat er nu nog een tweede Z-beeld van de rij an bestaat, G(z), dan geldt binnenhet convergentiegebied:

F (z)−G(z) =

∞∑n=0

an − anzn

= 0

Als het Z-beeld van een rij an bestaat, dan is het dus uniek.

33

6.3 Integraaltest reeksen

Het hieropvolgende bewijs behoort niet tot de leerstof, maar is me ’s nachts eens te binnengevallen (jammer genoeg bleek de Indier Madhava dit ook al gevonden te hebben). Hetkan dienen om de convergentie van de hyperharmonische reeks aan te tonen (zie verder).

StellingIndien de rij gedefinieerd door:

f : N→ N : n 7→ an

Uitbreidbaar is tot:f : R→ R : n 7→ an

Waarbij f monotoon en continu is in zijn domein en een vast teken bezit, dan geldt:

b+1∫a

f ≤b∑

n=a

an

Bewijs

n+1∫n

f ≤M(n+ 1− n)

n+1∫n

f ≤ an

b∑n=a

n+1∫n

f

≤ b∑n=a

an

b+1∫a

f ≤b∑

n=a

an

Voor de bovengrens kan op een analoge manier onderstaande ongelijkheid verkregen wor-den:

b∫a−1

f ≥b∑

n=a

an

34

Beschouw:

f : N→ R : x 7→x∑

n=1

1

n

Deze functie voldoet aan alle eerder vermelde voorwaarden. Bijgevolg wordt de bovengrensgegeven door ln(x) + 1 en de ondergrens door ln(x). Dit wordt grafisch bevestigd in degrafiek.

Doordat de ondergens divergent is, kan besloten worden dat de harmonische reeks di-vergent is. Op een analoge manier kan besloten worden dat de hyperharmonische reeksconvergent is als p > 1.Algemeen kan geconcludeerd worden dat als een functie f(x) voldoet aan de voorwaardenvan de stelling, dat deze convergent is als de integraal convergent is, en divergent als deintegraal divergent is.

0

2

4

6

8

10

0 2000 4000 6000 8000 10000

y

x

ln(x) + 1

f(x)

ln(x)

35

6.4 Tweede afgeleide

Bij het bewijs voor convexe functies is het noodzakelijk om een limietdefinitie te hebbenvan de tweede afgeleide. Deze kan als volgt opgesteld worden:

f ′(x) = lima→0

f(x+ a)− f(x)

a

Deze vergelijking kan dan gesubstitueerd worden in de limietdefinitie van de tweede afge-leide:

f ′′(x) = limb→0

f ′(x+ b)− f ′(x)

b

= lima,b→0

f(x+ a+ b)− f(x+ a)− f(x+ b) + f(x)

ab

Als deze limiet bestaat mag je a gerust = b nemen. Stel nu ook x+a = x, dan krijg je:

f ′′(x) = lima→0

f(x+ a)− 2f(x) + f(x− a)

a2

Merk trouwens op dat de definitie van de afgeleide ook via de Taylorvergelijking kan aan-getoond worden. Dit gaat als volgt: De eerste afgeleide is gedefinieerd als:

f ′(x) = lima→0

f(x+ a)− f(x)

a

Diezelfde definitie uitgeschreven met de Taylorvergelijking ziet er als volgt uit:

∞∑n=0

f (n+1)(x0)(x− x0)n

n!= lim

a→0

∞∑n=0

f (n)(x0) ((x+ a− x0)n − (x− x0)n)

a · n!

36

De correctheid hiervan aantonen gaat als volgt:

∞∑n=0

f (n+1)(x0)(x− x0)n

n!= lim

a→0

∞∑n=0

f (n)(x0) ((x+ a− x0)n − (x− x0)n)

a · n!

= lima→0

∞∑n=0

f (n)(x0)

((n∑k=0

(nk

)(x− x0)k · an−k

)− (x− x0)n

)a · n!

= lima→0

∞∑n=1

f (n)(x0)

(n−1∑k=0

(nk

)(x− x0)k · an−k−1

)n!

=∞∑n=1

f (n)(x0) · (x− x0)n−1 · nn!

=∞∑n=0

f (n+1)(x0) · (x− x0)n

n!

D.

37